数学:インデックス
https://nam-students.blogspot.com/2013/03/blog-post_5.html @
https://www.blogger.com/blog/post/edit/28938242/8021546353190676265
経済学関連:
正規分布
https://dylan2023bible.blogspot.com/2024/02/blog-post_88.html
例題で学ぶ 初歩からの計量経済学 白砂堤津耶(統計学初歩他)
NAMs出版プロジェクト: 最小二乗法(直線)の簡単な説明
http://nam-students.blogspot.jp/2017/10/blog-post_6.htmlNAMs出版プロジェクト: 長沼伸一郎『経済数学の直観的方法 マクロ経済学編』:目次
http://nam-students.blogspot.jp/2016/09/blog-post_17.html
経済数学の直観的方法 確率・統計編 (ブルーバックス)/長沼伸一郎
http://nam-students.blogspot.jp/2016/12/honto.html
| ||||||||||||||||||||||||
https://x.com/asunokibou/status/1757751699207561298?s=61
ブラックショールズ:熱伝導方程式 https://youtu.be/F_8XjAzUNxA
http://nam-students.blogspot.jp/2016/07/httpsyoutubef8xjazunxa.html
NAMs出版プロジェクト: ルベーグ積分 wikiより
http://nam-students.blogspot.jp/2016/01/blog-post_26.html
『経済数学の直観的方法 確率・統計編』(その1) 長沼伸一郎著 - …読書と旅の日記
http://blog.goo.ne.jp/clezio0/e/6852302432ab7de648a58e5018264f12/?cid=2d246c9f4613351264c257d6c96dabf3&st=0
『経済数学の直観的方法 確率・統計編』(その2) 長沼伸一郎著 -
http://blog.goo.ne.jp/clezio0/e/464e02c51ebdad4af1390e186684604f
経済数学の直観的方法 確率・統計編 (ブルーバックス)/長沼伸一郎 :honto
https://honto.jp/netstore/pd-book.html?prdid=28132003#productInfomation
【作図】ルートaを作図します!例題で√7の作図も!【初等幾何学】 https://youtu.be/DxVhWvXkXq4
https://freeassociations2020.blogspot.com/2022/09/finding-square-roots-geometrically.html
ゆっくり解説・数学史上最悪のミス!?なぜ円周率は直径を用いたのか?
https://freeassociations2020.blogspot.com/2021/12/blog-post_8.html
数式CM
http://nam-students.blogspot.com/2017/02/blog-post_18.html
https://nam-students.blogspot.com/2018/12/12-2018-12-5-251-3000-isbn-978-4-8010.html
ヘルマン・グラスマン
https://nam-students.blogspot.com/2019/02/blog-post_47.html
グラフ理論(ケーニヒスベルクの橋)関連:メモ
http://nam-students.blogspot.jp/2016/03/blog-post_11.html
四色問題
http://nam-students.blogspot.com/2019/03/blog-post_34.html
円錐曲線
http://nam-students.blogspot.com/2018/10/blog-post_82.html
「錐体の体積がなぜ1/3(3分の1)かを感覚的に納得させる方法」
http://nam-students.blogspot.jp/2015/08/1331.html
数学の世界地図
https://freeassociations2020.blogspot.com/2020/05/blog-post_6.html
ポアンカレ予想:メモ
http://nam-students.blogspot.jp/2016/03/blog-post_42.html
回転数http://nam-students.blogspot.com/2018/09/blog-post_6.html
正二十面体と正十二面体
http://nam-students.blogspot.jp/2015/07/blog-post_7.html
グロタンディーク、ABC予想:メモ
http://nam-students.blogspot.jp/2015/10/blog-post_17.html
ゴールドバッハ予想:メモ(&リーマン予想、素数関連)
http://nam-students.blogspot.jp/2014/03/blog-post_24.html
リーマン予想
http://nam-students.blogspot.com/2018/09/0926.html
フェルマーの最終定理と岩澤理論
https://freeassociations2020.blogspot.com/2020/05/blog-post.html
フィボナッチ数列
http://nam-students.blogspot.jp/2012/11/blog-post_25.html
ゲーム理論で解明されたユダヤの知恵
http://nam-students.blogspot.jp/2012/11/blog-post_28.html
Karinthy Frigyes Lancszemek フリジェシュ・カリンティ「鎖」1929
http://nam-students.blogspot.jp/2012/01/karinthy-frigyeslancszemek1929.html?m=0
https://nam-students.blogspot.com/2019/12/chain-links.html
NAMs出版プロジェクト: デカルトの四則演算:メモ
http://nam-students.blogspot.jp/2011/12/blog-post_25.html
デカルトによる量の次元の統一:メモ
http://nam-students.blogspot.jp/2012/10/blog-post_16.html
九九(作業中)
http://nam-students.blogspot.jp/2014/07/blog-post_12.html
数学体験館
http://nam-students.blogspot.jp/2014/08/2040808.html?m=0
数学関連:別ブログ
http://yojiseki.exblog.jp/i27/
数学記号の表wiki
http://ja.wikipedia.org/wiki/数学記号の表
NAMs出版プロジェクト: ルベーグ積分 wikiより
http://nam-students.blogspot.jp/2016/01/blog-post_26.html






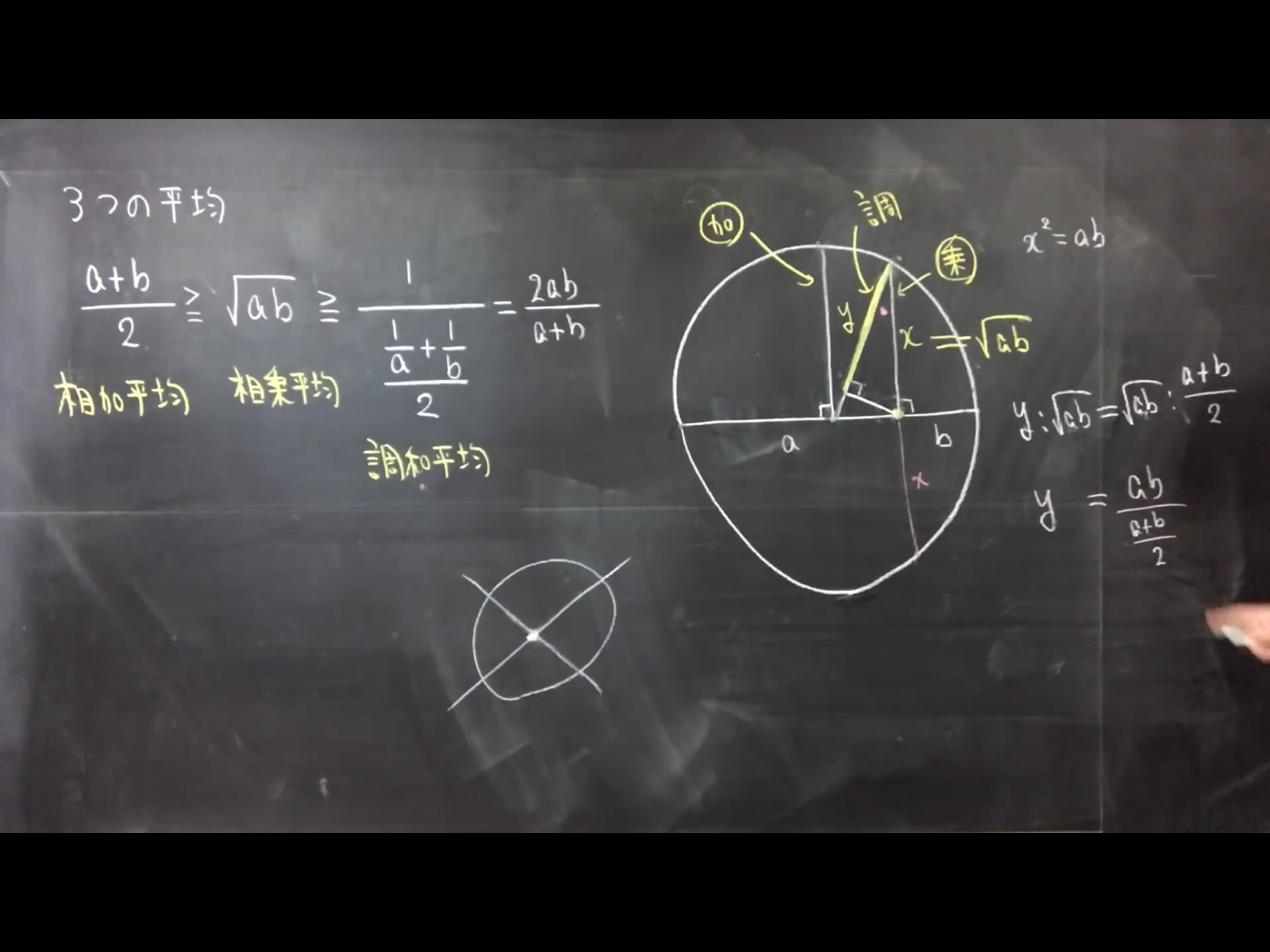


102 Comments:
━━━━━━┓
┃
┃
┃
┃
┃
━━━━━━┛
┏━━━━┓
┃ ┃ ┃
┗━┛ ┏━┛
┃
┏━┓ ┗━┓
┃ ┃ ┃
┗━━━━┛
┓┏━┓┏━┓
┏┛┗┓┗┛┏┛
┃┏┓┃┏┓┗┓
┗┛┗┛┃┗━┛
┏┓┏┓┃┏━┓
┃┗┛┃┗┛┏┛
┗┓┏┛┏┓┗┓
┛┗━┛┗━┛
1:55 午前
yoji said...
┏━┓┏━┓┏━┓┏━┓┏━┓
┗┛┏┛┗┓┗┛┏┛┗┓┗┛┏┛
┏┓┗┓┏┛┏┓┃┏┓┃┏┓┗┓
┃┗━┛┗━┛┃┗┛┗┛┃┗━┛
┗┓┏━━┓┏┛┏┓┏┓┃┏━┓
┏┛┗┓┏┛┗┓┃┗┛┃┗┛┏┛
┃┏┓┃┃┏┓┃┗┓┏┛┏┓┗┓
┗┛┗┛┗┛┗┛┏┛┗━┛┗━┛
┏┓┏┓┏┓┏┓┗┓┏━┓┏━┓
┃┗┛┃┃┗┛┃┏┛┗┓┗┛┏┛
┗┓┏┛┗┓┏┛┃┏┓┃┏┓┗┓
┏┛┗━━┛┗┓┗┛┗┛┃┗━┛
┃┏━┓┏━┓┃┏┓┏┓┃┏━┓
┗┛┏┛┗┓┗┛┃┗┛┃┗┛┏┛
┏┓┗┓┏┛┏┓┗┓┏┛┏┓┗┓
┗━┛┗━┛┗━┛┗━┛┗━┛
2:24 午前
yoji said...
上の図はペアノ(Peano)曲線と呼ばれるもので、下の図の左のように、最初の単純な曲線を半分に
縮小し、向きを変えて4枚貼り合わせます。
次に線で結びます。これを繰り返すとどんどん複雑になって無限に繰り返すと正方形を埋め尽くします。
自己相似形の繰り返しという意味でフラクタルになっています。
フラクタルの例 ペアノ曲線のつくり方
図の右側のように4枚張り合わせるときに少し隙間を空ける(半分ではなく隙間分考えて縮小しておく)
と下のようになりフラクタルらしいフラクタル図形になります。
http://math.artet.net/?cid=61002
山口昌哉『数学がわかるということ』(ちくま学芸文庫/2010年)より
-『食うものと食われるものの数学』(筑摩書房/1985年)が文庫化されたもの-
柿 の 実 西谷得宝
せどの柿の木に柿が十五なっていたげな
そこへ雀が八羽,椋鳥が五羽飛んできてあったげな.
それでみんなで二十八になったげな,
どうじゃな仏法とは,おおよそ
こんなもんじゃげな.
(p.35/ルビ省略)
この詩の作者である西谷得宝(にしたにとくほう)さんは秋田県出身のアララギ派の歌人で、若い間の大部分を托鉢僧として東北地方をはじめ、日本の各地を歩いた方だそうです。山口昌哉先生は西谷さんから直接、京都でこの詩をいただいたとのこと。数学者である自分は仏法(ほとけさまのおしえ)というものはよく知らないけれど、この詩があまりにも数学の本当のところをついていて、それを数学にほとんど関係のない方から示していただいたことに感激した、ということを書いておられます。
山口昌哉先生いわく、この詩は、数学がもつ、ものの見方の「あらさ」と「きちょうめんさ」の両方の性格を、よく表わしている、と。
ずっと遠くから見れば、背戸(勝手口)の柿の木に、何だか「もの」が、1つ、2つと数えて28個ある。実際に近くに寄ってみると、柿の実が15、スズメが8羽、そしてムクドリが5羽いるわけで、ここではちょっと足し算をする気にはなれないというもの。しかし、それらがほとんど「もの」としか見えないぐらいの位置から見られるならば、1つ、2つ、3つと数えることができる。そしてその計算の結果は28個であって、けっして27個でも29個でもない。
トーマス・ベイズ
Thomas Bayes
(トーマス・ベイズ)
1936年に出版された『生命保険の歴史』にあるベイズの肖像画。これが実際にベイズを描いているかどうかどうかは疑わしい[1]。これより前の肖像画や確実な肖像画は残っていない。
人物情報
誕生 1702年
イングランド、ロンドン
死没 1761年4月7日(59歳)
イングランド、ケント
国籍 イギリス
学問
研究分野 数学
署名
テンプレートを表示
トーマス・ベイズ(Thomas Bayes、1702年 - 1761年4月17日)はイギリスの長老派の牧師・数学者である。ベイズの定理の特殊な場合についての証明が死後発表されたことで知られる。
目次 [非表示]
1 経歴
2 脚注
3 参考文献
4 外部リンク
経歴 [編集]
トーマス・ベイズはロンドンで生まれた。1719年に論理学と神学を修めるためにエディンバラ大学に入った。国教徒でなかったために、オックスフォード大学やケンブリッジ大学には入れなかった。
ベイズの定理
ベイズの定理(ベイズのていり、英: Bayes' theorem)とは、条件付き確率に関し、トーマス・ベイズによって示された定理である。
ベイズ統計学においては基礎として利用され、いくつかの未観測要素を含む推論等に応用される。例えば、迷惑メールの発見・分類といった作業のコンピュータを用いた自動化(フィルタリング)等の情報工学上の情報ふるい分けにも利用されている。
目次 [非表示]
1 ベイズの定理
2 ベイズ統計学におけるベイズの定理
2.1 概要
2.2 批判
3 脚注
4 関連項目
5 外部リンク
ベイズの定理 [編集]
一般に、確率および条件付き確率に関して、下記の恒等式が成り立つ。
この定理はイギリスの牧師トーマス・ベイズ(1702年(?) - 1761年)によって発見され、ベイズの死後にリチャード・プライスによって1763年に発表され[1]、後にピエール=シモン・ラプラスによってその存在が広く認識されるようになった。
ベイズ統計学におけるベイズの定理 [編集]
概要 [編集]
事象Bのベイズ確率について、
P(B) = 事象Aが起きる前の、事象Bの確率(事前確率, prior probability)
P(B|A) = 事象Aが起きた後での、事象Bの確率(事後確率,条件付き確率, posterior probability,conditional probability)
とする。 ベイズの定理を使えば、事後確率 P(B|A) は下記に従って計算される。
すなわち、事象Aに関するある結果(データ)が得られたとすると、それを反映し、尤度P(A|B) の乗算によって、事象Bの確率は事前確率から事後確率へと更新される。なお事象Bの確率の観点からは、P(A) は規格化乗数としての意味しかない。
ベイズ統計学(およびベイズ決定理論)は上記の手続きにその基礎をおき、名前の由来ともなっている。
批判 [編集]
ベイズの定理は事前確率及び尤度を仮定した下で事後確率を与える、というあくまで相対的なメカニズムを表した定理にすぎない。したがって事後確率の計算結果の信憑性や有用性は、事前分布と尤度の設定にかかっており、慎重を期すことが必要である。これはベイズの定理を含むベイズ統計学が、不確実性を含む問題を人によって異なる確率を用いて定式化することを許容する主観確率 (subjective probability) という立場をとっていることによる。この立場はまだ解析対象となっていない新たな問題へのアプローチを可能にするという利点がある一方で、確率の決め方について客観性に欠けるという批判もある(客観確率)。
http://www.yasuienv.net/BayesIntro.htm
「本書」では、「風が吹けば桶屋が儲かる」を用いて、ベイズ定理とは何かを説明しようと試みている。
まず、ベイズの定理を日本語を使って表現すると、次の式になる。
「風が吹く」ときに「桶屋が儲かる」確率 × 「風が吹く」確率
「桶屋が儲かる」ときに「風吹く」確率=----------------------------------------------------
「桶屋が儲かる」確率
この式は、例えば、昨年のデータを次のように仮定し、
風が吹いた日数=100日
桶屋が儲かった日数=10日
風が吹いて、かつ、桶屋が儲かった日数=5日
図1 桶屋が儲かるベン図
上のようなベン図を描いてみれば、一目瞭然である。「本書」には場合の日数が書いてないが、集合論もそうだし、確率論の確実な理解は、割合(%)などでなく、実際の「場合の数」を考えることによって、誤解をする可能性を大幅に減らすことができる。
「桶屋が儲かる」確率とは、本来、1年の内で、何日か桶屋が儲かったという事実から計算される数値で、分母には365日が使われた確率であろう。
昨年「桶屋が儲かった」日の確率(割合)=「桶屋が儲かった日数」/365日
「風が吹いた」確率も同様で
昨年「風が吹いた」日の確率=「風が吹いた日数」/365日
しかし、1年365日は共通の分母なので、すべてを確率で議論するときには、省くことも可能である。そこで、日数で議論を進めることにする。
となれば、上式において、
「風が吹いて桶屋が儲かった日」というのは、桶屋が儲かった日で、かつ、風が吹いた日なので、5日。
「風が吹く」ときに「桶屋が儲かる」確率は、桶屋が儲かった日数/風が吹いた日数である。すなわち、=5/100。
「風が吹く」確率は風が吹いた日数=100日。
「桶屋が儲かる」確率は桶屋が儲かった日数=10日。
結局 5/10=5/100 × 100 / 10 という恒等式が成立することになる。これが、ベイズの定理である。
これがベイズ関係の書籍などでは、すでに示した式のように記述されている。
どのような記事を書くにしても、まず、何か、ベイズ推定の本を買わなければならない。アマゾンをいろいろとさまよってみて、超入門書らしきものを探してみた。結果としてたどり着いたのは、「Excelでスッキリわかる ベイズ統計入門」。涌井良幸、涌井貞美著、日本実業出版社、2010年10月20日、2200円を買ってみた。以下、「本書」と記述することにする。
以下の文章で、「本書」の構成と一部に見られる論理矛盾を指摘するが、他のベイズ推計の本を見ていないで、すべてのこのジャンルの本がこのように妙な点があるということを言っている訳ではないことをあらかじめご了解いただきたい。
━━━━━━┓
┃
┃
┃
┃
┃
━━━━━━┛
┏━━━━┓
┃ ┃ ┃
┗━┛ ┏━┛
┃
┏━┓ ┗━┓
┃ ┃ ┃
┗━━━━┛
┓┏━┓┏━┓
┏┛┗┓┗┛┏┛
┃┏┓┃┏┓┗┓
┗┛┗┛┃┗━┛
┏┓┏┓┃┏━┓
┃┗┛┃┗┛┏┛
┗┓┏┛┏┓┗┓
┛┗━┛┗━┛
上の図はペアノ(Peano)曲線と呼ばれるもので、最初の単純な曲線を半分に縮小し、向きを変えて4枚貼り合わせます。
次に線で結びます。これを繰り返すとどんどん複雑になって無限に繰り返すと正方形を埋め尽くします。
自己相似形の繰り返しという意味でフラクタルになっています。
http://homepage3.nifty.com/SGL/FRACTAL/
┏━┓┏━┓┏━┓┏━┓┏━┓
┗┛┏┛┗┓┗┛┏┛┗┓┗┛┏┛
┏┓┗┓┏┛┏┓┃┏┓┃┏┓┗┓
┃┗━┛┗━┛┃┗┛┗┛┃┗━┛
┗┓┏━━┓┏┛┏┓┏┓┃┏━┓
┏┛┗┓┏┛┗┓┃┗┛┃┗┛┏┛
┃┏┓┃┃┏┓┃┗┓┏┛┏┓┗┓
┗┛┗┛┗┛┗┛┏┛┗━┛┗━┛
┏┓┏┓┏┓┏┓┗┓┏━┓┏━┓
┃┗┛┃┃┗┛┃┏┛┗┓┗┛┏┛
┗┓┏┛┗┓┏┛┃┏┓┃┏┓┗┓
┏┛┗━━┛┗┓┗┛┗┛┃┗━┛
┃┏━┓┏━┓┃┏┓┏┓┃┏━┓
┗┛┏┛┗┓┗┛┃┗┛┃┗┛┏┛
┏┓┗┓┏┛┏┓┗┓┏┛┏┓┗┓
┗━┛┗━┛┗━┛┗━┛┗━┛
http://www005.upp.so-net.ne.jp/yoshida_n/qa_a18.htm
19世紀までに確立される近代解析では、実数の演算に基づいて極限や連続を扱ってきましたが、いわゆる現代数学になると、抽象的な空間に適当な構造を与えることによって極限や連続の概念を定義し、これを元にそれまでの解析学と同様な理論を展開するのが一般的になっています。こうした抽象的な「位相空間(topological space)」──ハウスドルフ空間は、異なる2点が決してくっついていないような位相空間で、2点間の距離が定義できる位相空間(距離空間)はハウスドルフ空間の一種です──を利用すると、ユークリッド空間のような具体的な空間が持つ特殊性に縛られずに、数学の手法を使って一般的な性質を調べることができます。例えば、フラクタルという概念は、純粋数学の研究対象にとどまらず、相転移など非線形な物理過程の解明、ひび割れ・放電・凝集などのパターン解析、素材の質感(テクスチャ)や土壌の間隙率の評価、コンピュータ・グラフィクスの作成など、さまざまな方面に応用できるもので、特定の空間を仮定しない方が扱いやすいのです。
位相空間とフラクタル次元の関係はかなり高度な数学の領域に属しますので、本格的な説明は数多く出版されている参考書に譲るとして、ここでは、フラクタル次元とはどういうものかを直感的に紹介するだけにしておきましょう。
フラクタルとは、数学者マンデルブロが1975年に提唱した概念で、簡単に言うと、拡大・縮小によって観測のスケールを変えても同じように見える図形のことです。右の図は有名なマンデルブロ図形の一部ですが、上の図の四角に囲まれた部分を拡大すると相似的な下の図になることを示しています(宮根裕司氏のフラクタル描画ソフト “MandelPalette 1.1”で描いた絵を256色に減色しています)。こうした自己相似性を持つ図形の次元は、通常の線(1次元)や面(2次元)と同じように定義することはできません。実際、マンデルブロ図形の縁は、いくら拡大してもなめらかな曲線にはならずに複雑にゆらめいていて、1次元の線とも2次元の面ともつかないものになっているのです。
こうしたフラクタル図形の次元を定義するために案出されたのが、フラクタル次元という概念です。フラクタル次元の厳密な定義には数学のテクニックが必要になりますが、凝集パターンなど実験的に得られた図形のフラクタル次元を推測するには、ボックス・カウンティング(Box-counting)という簡単な方法が使われます。これは、図1に示すように曲線を1辺の長さLの正方形(3次元の場合は立方体)のボックスで覆い、曲線を含むボックスの個数N(L)を求めるというものです。ここで、1辺の長さを変化させたとき、
N(L) = C・L-D (Cは定係数)
という関係式が(良い近似で)成り立つ場合、Dをフラクタル次元と定義します。図1では曲線を含むボックスは影を付けた14個ですが、1辺の長さを半分にした図2では27個になっているので、D=1と推測されます(実際には、もう少しサンプルを多く取らなければなりません)。
フラクタル次元が1より大きくなる曲線の最初の例は、ペアノが創案しヒルベルトが簡単な作り方を提示したペアノ曲線でしょう(下図)。これは、初めにコの字型の図形から出発し、正方形のボックスの中の部分を一定の方法で段階的に変形していくことによって得られる曲線で、1本の線で平面を完全に埋め尽くしてしまうものです。実際、ボックス・カウンティング法によれば、曲線が全てのボックスを通過しており、正方形の1辺を半分にすると曲線が通過しているボックスの数が4倍に増えることから、フラクタル次元が2になることがわかります。
もう一つの有名な例がコッホ曲線と呼ばれるもので、右図のように線分を3等分し真ん中の部分を正三角形の2辺で置き換える操作を繰り返すことによって生成される曲線です。コッホ曲線のフラクタル次元は、1.26…になることが知られています。
このコメントは投稿者によって削除されました。
プラトン立体とケプラー・ポアンソ立体 | METATRONIC METALOGUE
http://metalogue.jugem.jp/?eid=1830
プラトン立体とケプラー・ポアンソ立体
2013.04.22 Monday ■多面体と多様体の世界 00:01 comments(2) - by 小野満麿
■正3角形と正方形は、すぐ隣りの頂点を飛び越して頂点をつないだ図形を描こうとしても不可能だ。正5角形で初めて5芒星が描け、正6角形には正3角形2つからなる6芒星が描ける。正7角形には1つ飛ばしの太った7芒星と2つ飛ばしの痩せた7芒星が描け、正8角形には1つ飛ばしで正方形2つからなる8芒星、2つ飛ばしでひと筆書きの8芒星ができる。以下、正9角形以降も同様に多芒星が描ける。
■2次元平面の多角形には1角形・2角形がなく3番目の3角形から始まっている。同様に多芒星には3芒星・4芒星がなく3番目の5芒星から始まっている。3次元空間のプラトン立体とケプラー・ポアンソ立体の関係もこの多角形と多芒星の関係に似ている。ただしプラトン立体にはさらに面の数が正3・4・5角形だけに限られ、そして点に集まる線の数も3・4・5本だけが許されるという制限があった。
■プラトン立体には、正4面体・正6面体・正8面体・正12面体・正20面体の5種類しか知られてなかった。しかしケプラーは正12面体と正20面体の辺を星型化することにより、1619年に小星型12面体と大星型12面体の2つを発見した。またほぼ2世紀後の1809年に、ポアンソがその双対立体である大12面体と大20面体の2つを発見した(※1)。この4立体をまとめてケプラー・ポアンソ立体と呼ぶ。
■プラトン立体とケプラー・ポアンソ立体の最大の違いは、前者が凸多面体であるのに対し後者は凹多面体であるということだ。なお正12面体と正20面体及び4つのケプラー・ポアンソ立体は、みな黄金比を生む5重回転対称性を持つ。ここでこの9立体を戯れに10進法の1~5まで及び6~9までの数と対応させてみる発想は、さほど悪趣味ではなかろう。なお数字の0に当たるものには球体を据えてみた。
■プラトン立体の定義を緩めて、面が同一ではなく複数の正多角形でも良いアルキメデス立体は13種類あった。この双対立体のカタラン立体も13種類あるので合わせると26種類になる。また全ての面が正3角形の凸多面体のデルタ多面体は全部で8種類(3種類はプラトン立体)ある。さらに面が全て同一の菱形のみで構成されている等面菱形多面体は4種類存在する。星型多面体はここでは言及しない。
■全ての面が正多角形で全ての辺の長さが等しい凸多面体のうちで、プラトン立体・アルキメデス立体・アルキメデスの角柱・アルキメデスの反角柱を除いた立体をジョンソン・ザルガラー立体と言う。これらは全部で92種類あるが、この92という数は自然界に存在する最大の元素ウランの原子番号(陽子数)や、正4面体を除く4つのプラトン立体の面と点の総和数などを想起させる興味ある数である。
…………………………………………………………………………………………
(※1)1811年にオーギュスタン=ルイ・コーシーが星型正多面体は全部でこの4種類しかないことを証明した。
http://ronri2.web.fc2.com/hanron04.html
●論理的思考法―逆と裏と対偶
ここでは論理の欠陥(前提と結論のつながり方のミス)を見抜くための基礎知識として、『逆』と『裏』と『対偶』を解説します。
『AならばBである』という文に対して、
『BならばAである』を「逆」と呼び、
『AでなければBでない』を、「裏」と呼び、
『BでなければAでない』を、「対偶」と呼びます。
『AならばBである』が真実であるとき、『対偶』は常に真実です。しかし『逆』と『裏』は真実であるとは限りません。これは、「A」を「女」に、「B」を「人間」に置き換えて考えてみれば分かりやすいでしょう。
『女ならば人間である』が真実のとき、
逆は、『人間ならば女である』ですが、これは真実ではありません。(男かもしれませんから)
裏は、『女でなければ人間でない』ですが、これも真実ではありません。(男も人間ですから)
対偶は、『人間でなければ女でない』です。これは真実です。
では、しっかりと理解するために次の問題を解いてください。
ヒント!
・「逆」はAとBの位置が入れ替わります。
・「裏」はAとBの否定形 肯定形が裏返ります。
・「対偶」はAとBの位置が入れ替わって、さらに否定形 肯定形も裏返ります。
【問題1】
次の主張の逆・裏・対偶を答えてください。(答えは「 」内をドラッグ)
http://bladerunner.tou3.com/Entry/659/
数学者の秋山仁は、中学高校までの数学だったか、とにかく数学ができるためには
次の四つの能力があれば十分だ、とどこかで書いていた。
1 下駄箱に靴をそろえて入れることができる
2 辞書が引ける
3 カレーライスが作れる
4 最寄駅から自宅までの地図が描ける
1の靴をそろえられるということは「1対1の対応」の概念が理解できているということで、
2の辞書が引ける、すなわち辞書で目的の単語を見つけられるというのは「順序」の概念が
分かっているということであり、
3のカレーが作れるというのは「手順を整理し観察・実行」ができるということを意味し、
4の地図が描けるということは「抽象能力」がある(3次元のものを2次元に移して
考えられる、よけいな風景を省いて道順だけ抜き出して描ける、といった)
……という意味だそうだ。
http://twilog.org/Khatru/date-130411
4月11日
khatru@Khatru
辞書をちゃんと引けるか否かでチェックできる。このくらいのことができれば、あとはコツコツ努力すれば、フィールズ賞とまではいかないかもしれないが、大学入試の数学なんかヘッチャラですよと、いいかげんな話をしたら、翌日の朝日新聞の社説にそのことが書かれちゃった"
posted at 22:28:40
4月11日
khatru@Khatru
"地図を描けるというのは抽象能力があるということです。だって、三次元のユークリッド空間のものを平面に帰着させるんだから。また、一対一の対応が下駄箱のテストでわかる。さらに、観察能力がカレーライスをつくれるか否かで試せるし、順序関係を把握する能力があるか否か
posted at 22:28:33
4月11日
khatru@Khatru
"微積分が好きだなんて言う学生は、数学科に向いてないんじゃないかな。だって、本物の微積分ならいいけれど、極限値にしても、「限りなく何とかに近づく」なんていう、あいまいなものだ。「限りなく君を愛す」みたいで文学的な表現だよ。" 『秋山仁の遊びからつくる数学』
http://twilog.org/Khatru/date-130411
"微積分が好きだなんて言う学生は、数学科に向いてないんじゃないかな。だって、本物の微積分ならいいけれど、極限値にしても、「限りなく何とかに近づく」なんていう、あいまいなものだ。「限りなく君を愛す」みたいで文学的な表現だよ。"
"地図を描けるというのは抽象能力があるということです。だって、三次元のユークリッド空間のものを平面に帰着させるんだから。また、一対一の対応が下駄箱のテストでわかる。さらに、観察能力がカレーライスをつくれるか否かで試せるし、順序関係を把握する能力があるか否かは辞書をちゃんと引けるか否かでチェックできる。このくらいのことができれば、あとはコツコツ努力すれば、フィールズ賞とまではいかないかもしれないが、大学入試の数学なんかヘッチャラですよと、いいかげんな話をしたら、翌日の朝日新聞の社説にそのことが書かれちゃった"
『秋山仁の遊びからつくる数学』
http://twilog.org/Khatru/date-130411
"微積分が好きだなんて言う学生は、数学科に向いてないんじゃないかな。だって、本物の微積分
ならいいけれど、極限値にしても、「限りなく何とかに近づく」なんていう、あいまいなものだ。
「限りなく君を愛す」みたいで文学的な表現だよ。"
"地図を描けるというのは抽象能力があるということです。だって、三次元のユークリッド空間の
ものを平面に帰着させるんだから。また、一対一の対応が下駄箱のテストでわかる。さらに、観察
能力がカレーライスをつくれるか否かで試せるし、順序関係を把握する能力があるか否かは辞書を
ちゃんと引けるか否かでチェックできる。このくらいのことができれば、あとはコツコツ努力すれ
ば、フィールズ賞とまではいかないかもしれないが、大学入試の数学なんかヘッチャラですよと、
いいかげんな話をしたら、翌日の朝日新聞の社説にそのことが書かれちゃった"
『秋山仁の遊びからつくる数学』
http://bladerunner.tou3.com/Entry/659/
http://twilog.org/Khatru/date-130411
"微積分が好きだなんて言う学生は、数学科に向いてないんじゃないかな。だって、本物の微積分
ならいいけれど、極限値にしても、「限りなく何とかに近づく」なんていう、あいまいなものだ。
「限りなく君を愛す」みたいで文学的な表現だよ。"
"地図を描けるというのは抽象能力があるということです。だって、三次元のユークリッド空間の
ものを平面に帰着させるんだから。また、一対一の対応が下駄箱のテストでわかる。さらに、観察
能力がカレーライスをつくれるか否かで試せるし、順序関係を把握する能力があるか否かは辞書を
ちゃんと引けるか否かでチェックできる。このくらいのことができれば、あとはコツコツ努力すれ
ば、フィールズ賞とまではいかないかもしれないが、大学入試の数学なんかヘッチャラですよと、
いいかげんな話をしたら、翌日の朝日新聞の社説にそのことが書かれちゃった"
『秋山仁の遊びからつくる数学―離散数学の魅力』 (ブルーバックス1994/02)
http://bladerunner.tou3.com/Entry/659/
https://www.nhk-ondemand.jp/goods/G2011027278SA000/
ハイビジョン特集 数学者はキノコ狩りの夢を見る ~ポアンカレ予想・100年の格闘~
特選ライブラリー
お試し視聴をする
難問の「ポアンカレ予想」を解き、姿を消した天才数学者の行方は?「NHKスペシャル 100年の難問はなぜ解けたのか~天才数学者 失踪(しっそう)の謎~」の拡大版。
2007年放送(本編: 110分)
視聴期間:購入後3日0時間 購入期限:2014年3月31日
※クリックするとNHKサイトを離れます
単品210円(税込み)
http://ja.wikipedia.org/wiki/ポアンカレ予想
概要[編集]
ポアンカレ予想とは、
単連結な3次元閉多様体は3次元球面 に同相である。
という予想であり、1904年にフランスの数学者アンリ・ポアンカレによって提出された。以来ほぼ100年にわたり未解決だったが、2002年から2003年にかけてロシア人数学者グリゴリー・ペレルマンはこれを証明したとする複数の論文をarXivに掲載した。これらの論文について2006年の夏ごろまで複数の数学者チームによる検証が行われた結果、証明に誤りのないことが明らかになり、ペレルマンには、この業績によって2006年のフィールズ賞が贈られた(ただし本人は受賞を辞退)。
一般化された問題[編集]
単連結な2次元閉多様体においては、どのような輪であっても引き絞れば回収できるようであれば、その表面(表皮部分)は2次元球面に同相である。
ポアンカレ予想は一般化(高次元に拡張)できる。それは次のようなものである。
n次元ホモトピー球面はn次元球面に同相である
このようにポアンカレ予想をn次元に一般化するとn=2での成立は古典的な事実であり、n≧4の場合は早くに証明が得られていた。n≥5の時はスティーヴン・スメイルによって(1960年)、n=4の時はマイケル・フリードマンによって(1981年)証明された。2人とも、その業績からフィールズ賞を受賞している。スメイルの証明は微分位相幾何学的なものであったが、フリードマンの証明は純粋に位相幾何学的なものである。実際、フリードマンの結果はその直後にドナルドソンによる異種4次元ユークリッド空間(位相的には通常の4次元空間だが、微分構造が異なるもの)の発見へとつながった。以上よりオリジナルである3次元ポアンカレ予想のみを残し、高次元ポアンカレ予想は先に決着してしまった(微分同相については4次元ポアンカレ予想も未解決)。
数学的に厳密ではないが、次のように例えることができる。宇宙の中の任意の一点から長いロープを結んだロケットが宇宙を一周して戻って来たとする。ロケットがどんな軌道を描いた場合でもロープの両端を引っ張ってロープを全て回収できるようであれば、宇宙の形は概ね球体である(ドーナツ型のような穴のある形、ではない)と言えるのではないか、というのが(3次元)ポアンカレ予想の主張である。[独自研究?]
□introduce
「ε-δ論法」を聞いたことがあるだろうか.
(ε:イプシロン,δ:デルタ)
高校で理系だった人なら,関数の「連続」や「収束」という言葉が記憶にあるはずだ.
それを学ぶときは高校では,「無限大」や「無限小」という
数Ⅲ極限特有の考え方をつかって理解していたことだろう.
しかし,「連続」とは、ただ単に「途切れずに繋がっている」
という曖昧なものでは許されない.
つまり,「連続」や「収束」の定義は、もっと厳密なものが必要なのだ.
ここで,微積分の歴史を見てみる.
「微分積分学」を創設したのは、ニュートンやライプニッツである.
創設した当時は,「無限大」という実数の範囲では定義できない概念を使っていて,
18世紀になって,オイラーが発展させても,この点だけは改善されなかった.
級数の発散や収束に関しては,無頓着なままで理論を発展させていったため、
誤った結論に導かれてしまうことがしばしばあった.
そこで登場するのが「ε-δ 論法」である.
19世紀になってカール・ワイエルシュトラスがこれを完成させて、
これによって「無限小」や「無限大」という概念を一切出さずに
収束・連続を「厳密に」定義できるようになったのである.
しかしライプニッツ流の無限小・無限大を用いる解析も超実数を用いることで
現代では正当化されていて,「超準解析」や「無限小解析」と呼ばれる.
理系大学生が数学を学ぶときに,まず一番最初にぶつかる問題は
この「ε-δ論法」を用いて関数の連続性や数列の収束の
厳密な証明が介入してくる当たりである.
しかし,先に述べた通り,「連続」や「収束」を厳密に定義する必要がある以上,
ここを曖昧にしてはいけないのである.
確かに,厳密な議論は難しいが,
曖昧な言葉の定義を式で正確に表せることがこの論法の利点なのだ.
□「ε-δ論法」
○ε-δ論法の式
極限の式:「x→aのとき,f(x)→b」⇔「lim(x→a) f(x)=b」
ε-δ論法:「∀ε> 0,∃δ> 0 s.t.∀x∈R , | x-a | 0, ∀δ>0 s.t. ∃x∈R ,| x-a | ε1・・・(③)(ε1=ε0/10など)
そのときでも,同様に対応するδ1が存在して,
0 < |x-a| 0, ∃δ>0 s.t. x∈R, 0<|x-2|<δ」⇒「|x^2-4|<ε」が成立する.
これで,x→2のときx^2→4となることがε-δ論法によって示された.
(未完成です.①2012/03/01 5:10 ②2012/03/02 2:14)
http://note.chiebukuro.yahoo.co.jp/detail/n38327
http://teenaka.at.webry.info/200611/article_27.html
『親族の基本構造』での群論_(1)
<< 作成日時 : 2006/11/27 00:06 >>
ブログ気持玉 1 / トラックバック 1 / コメント 10
「思想の中の数学的構造」(山下正男著:ちくま学芸文庫)を入手しました。
この中にあのレビィ=ストロースの大著『親族の基本構造』の中のアンドレ・ヴェイユの考察を説明しています。
そうか、レビィ=ストロースに協力した数学者はアンドレ・ヴェイユでしたか。ブルバキの一員で、哲学者シモーヌ・ヴェイユのお兄さんでしたね。
実際問題、『親族の基本構造』は読めませんね。この本を読んでその概要を少しづつ理解してみたいと思います。
さて、一言で言ってしまうと、
「オーストラリアのカリエラ族における親族関係の中にクラインの四元群がひそんでいる」
「タラウ族における親族関係の中に4位の巡回群がひそんでいる」
ということになります。
カリエラ族は部族内にA、B、C、Dの4つのセクションを持っています。
「Aに属する男性はBに属する女性としか結婚できず、この二人の間に生まれた子供はDに属する」
などという規則があります。
全部を書き出すと、
夫の所属 妻の所属 子の所属
-------- -------- --------
A B D
C D B
D C A
B A C
ということだそうです。なにやら構造的なものが見えてきそうですね。
子供のことはさておいて、結婚に関して言えば、次の4タイプがあることになります。
タイプ 夫 妻
---- -- --
M1 A B
M2 C D
M3 D C
M4 B A
つまり、この4タイプのいずれかに属さないと結婚が成立しない訳です。
さてこの4タイプのカップルの間に生まれた子の結婚タイプは何になるのでしょうか?
これは男と女では違ってきますね。
M1→D :♂の場合M3、♀の場合M2
M2→B :♂の場合M4、♀の場合M1
M3→A :♂の場合M1、♀の場合M4
M4→C :♂の場合M2、♀の場合M3
これを関数表示で、♂の場合をf(Mi)、♀の場合をg(Mi) と書くことにすると、
f(M1)=M3 ; g(M1)=M2
f(M2)=M4 ; g(M2)=M1
f(M3)=M1 ; g(M3)=M4
f(M4)=M2 ; g(M4)=M3
となります。まずfに注目すると、
f(f(M1))=f(M3)=M1
f(f(M2))=f(M4)=M2
f(f(M3))=f(M1)=M3
f(f(M4))=f(M2)=M4
となり、2代続いた男は同じ結婚タイプになります。これを f2=e と表現します。
今度はgに注目すると、
g(g(M1))=g(M2)=M1
g(g(M2))=g(M1)=M2
g(g(M3))=g(M4)=M3
g(g(M4))=g(M3)=M4
となり、2代続いた女は同じ結婚タイプになります。これを g2=e と表現します。
今度はgとfの組み合わせを見てみます。
f(g(M1))=f(M2)=M4 : g(f(M1))=g(M3)=M4
f(g(M2))=f(M1)=M3 : g(f(M2))=g(M4)=M3
f(g(M3))=f(M4)=M2 : g(f(M3))=g(M1)=M2
f(g(M4))=f(M3)=M1 : g(f(M4))=g(M2)=M1
となり、ここから見えてくるのは、 fg=gf という関係です。
ここで、仮に h≡fg=gf として乗積表を作ってみると
h2=fggf=fef=ff=e、hf=gff=ge=g、hg=fgg=fe=f、fh=ffg=g、gh=ggf=f なので
* | e f g h
------------
e | e f g h
f | f e h g
g | g h e f
h | h g f e
となり4元群を成すことがわかります。
結婚タイプ間の関係を考えると、
f
M1 ⇔ M3
g↓↑ ↓↑g
M2 ⇔ M4
f
これで、クラインの四元群が明らかになりました。
http://teenaka.at.webry.info/200611/article_28.html
『親族の基本構造』での群論_(2)
<< 作成日時 : 2006/11/28 00:12 >>
ブログ気持玉 0 / トラックバック 0 / コメント 0
カリエラ族における親族関係の中に「クラインの四元群」を見出しただけでは仕方が無いのです。
ここから推論してなにが導かれるのかが問題でしょう。
カリエラ族には不思議な婚姻ルールがありました。
「自己は母の兄弟の娘ないし父の姉妹の娘と結婚すべし」
これは「両側交叉イトコ婚」というになります。
「母の兄弟の娘」の場合
このときは f(g(Mi)) と g(f(Mi)) とのカップルになる訳です。
fg=gf なので、必然的に同じ結婚タイプになります。
「父の姉妹の娘」 の場合
このときは f(f(Mi)) と g(g(Mi)) とのカップルになる訳です。
f2=g2=e なので、必然的に同じ結婚タイプになります。
このように、「クラインの四元群」であると、必然的に「両側交叉イトコ婚」となることになります。
http://teenaka.at.webry.info/200611/article_30.html
『親族の基本構造』での群論_(3)
<< 作成日時 : 2006/11/30 07:01 >>
ブログ気持玉 0 / トラックバック 0 / コメント 0
今度「タラウ族における親族関係の中に4位の巡回群がひそんでいる」ということを考えましょう。
タラウ族も部族内にA、B、C、Dの4つのセクションを持っています。
規則を全部書き出すと、
夫の所属 妻の所属 子の所属
-------- ------- --------
A B A
B C B
C D C
D A D
ということだそうです。結婚に関して言えば、次の4タイプがあることになります。
タイプ 夫 妻
---- -- --
M1 A B
M2 B C
M3 C D
M4 D A
つまり、この4タイプのいずれかに属さないと結婚が成立しない訳です。
さてこの4タイプのカップルの間に生まれた子の結婚タイプは何になるのでしょうか?
これは男と女では違ってきますね。
M1→A :♂の場合M1、♀の場合M4
M2→B :♂の場合M2、♀の場合M1
M3→C :♂の場合M3、♀の場合M2
M4→D :♂の場合M4、♀の場合M3
これを関数表示で、♂の場合をf(Mi)、♀の場合をg(Mi) と書くことにすると、
f(Mi)=Mi
となり、f=e であり、
g(g(g(g(M1))))=g(g(g(M4)))=g(g(M3))=g(M2)=M1
なので、 g4(M1)=M1 ですが、これはどのタイプでも同じで g4(Mi)=Mi が言えます。
よって、 g4=e となります。
つまり巡回群になります。
結婚タイプ間の関係を考えると、
g
M4 ← M1
g↓ ↑g
M3 → M2
g
fとgの関係を考えると、ff≠gf、ff≠gg、gf≠gg、fg=gf となり、「片側交叉イトコ婚」しか成り立たないことになります。
http://teenaka.at.webry.info/200612/article_3.html
『親族の基本構造』での群論_(4)
<< 作成日時 : 2006/12/03 00:08 >>
ブログ気持玉 0 / トラックバック 0 / コメント 0
レヴィ=ストロースが考察したもう一つの群構造の例を見てみましょう。
彼は、考えられるもっとも単純な親族を「親族のアトム」と呼びました。
この下図の左側のようなものです。
この「アトム」は夫婦、兄妹、父子、伯父甥の4つの関係からなるもので、これを下図の右側のようなマトリックスで表わすことにします。
つまり、上の段「夫婦、兄妹」で同世代の関係、下の段「父子、伯父甥」は世代間の関係を表わしています。
それで、レヴィ=ストロースはこのアトムの中に4つのタイプがあると言います。
これらのマトリックスで親和である関係と反発関係が次の図のようになるということです。
(+)は親和関係、(-)は反発関係を示し、部族ごとにこのいずれかのタイプになるということです。
例として、
(1)→メラネシアのトロブリアント
(2)→ブーガンヴィル島のシウアイ
(4)→コーカサスのチエルケッス
などが紹介されていました。(3)は無いのですが。。
さて、数学的構造はこの次にします。
http://teenaka.at.webry.info/200612/article_14.html
『親族の基本構造』での群論_(5)
<< 作成日時 : 2006/12/14 00:10 >>
ブログ気持玉 0 / トラックバック 0 / コメント 0
この前の記事から大分経ってしまいましたが、親族のアトムの親密/親和関係の4種類を示しましたが、これらの間には3種のシンメトリーが存在し、クラインの4元群を成す
ことを示します。
ところで、クラインの4元群について説明していませんでしたが、乗積表を示しましょう。
「e」を単位元として、
e L M N
------------------
e | e L M N
L | L e N M
M | M N e L
N | N M L e
という関係になります。
で、親族のアトムの親密/親和関係をマトリクスで表わして、関係を図示すると次のようになります。
この本「思想の中の数学的構造」(山下正男著:ちくま学芸文庫)では、この図だけでクラインの4元群を成すとしています。
ちょっと説明が物足りませんね。
そこで、+と-で示したマトリクスを+1と-1で表わしたときに変換行列をLMNを求めてみました。
M=[ 1 0 0 -1 ]
L=[ -1 0 0 1 ]
N=[ -1 0 0 -1 ]
上図の関係を満たしており、クラインの4元群乗積表も満たしていると思います。多分。。。
499 2/17(月)12:16 0↓
構造主義とは数学の本質を社会の本質に置き換えるモデル。
ポアンカレは言う。
「数学者は対象を研究しない。研究するのは対象間の関係である。
だからその関係が変わらないかぎり、これらの対象を別の対象でおきかえることには
無頓着である。数学者は質料には無関心であり、ただ形相だけが関心を引く」
(ポアンカレ著『科学と仮説』河野伊三郎訳 岩波文庫 43頁)
330 2/8(土)09:46 0
ウィキのポアンカレ回帰定理の項目からの引用
解析力学では力学系のひとつの状態は位相空間(例えば質点の位置と運動量を
座標とする空間)上の点で表され、その点の近傍はその状態に近い状態の集ま
りを表し、回帰定理はこの位相空間上の力学系に関する定理である。簡単に
は、「力学系は、ある種の条件が満たされれば、その任意の初期状態に有限
時間内にほぼ回帰する」[5]、「ほとんどすべての軌道が出発点の任意の近傍
に無限回もどってくる」[4]、「与えられた初期条件に、いくらでも近づき、
かつそれを何回でも繰返すことができる」[2]と表現される
永遠回帰の力学版である。ハイデガー、ドゥルーズらは、この定理を当然知っていて、
明らかにそのニーチェ解釈に影響していると思われる。
むかし、ニーチェ永遠回帰のネタがこれだという文章を読んだことがあったが、
じつはニーチェが本に書いたのは、ポアンカレ論文よりも五年早かったので、パクリではないようだ。
その逆もたぶんないだろう。
http://www.edu.city.hashimoto.wakayama.jp/gakkyou/kouen.pdf#search='不定域イデアル'
§5 以上の準備の元に岡潔がどのような数学の発見をしたのか説明をいたします。岡潔の業績は、ある
ドイツの数学者をして、「岡というのは個人の名前ではなく、複数の数学者のグループ名ではないのか」 と言わしめたほどですので、簡単に紹介できるものではありませんが、様々な発見の中でも、特に重 要で、その後の数学に莫大な影響を与えた発見についてお話しします。
それは一言で言うと、図形が与えられたとき、その部分的(局所的)なデータと、全体的(大域的) なデータとを結びつける数学的な言葉=概念を発明したことです。この理論を岡潔は不定域イデアル の理論とよびましたが、今では層の理論と呼ばれています。
現在では誰もが、宇宙からの写真を見て、地球が丸いと信じていますが、外から地球を見られない 時、私たちはどのようにして、私たちが住んでいる世界の形を知ることができるでしょうか。マゼラ ン一行が地球一周の航海から帰って来たことで、地球は丸いと結論できますでしょうか。
もし私たちが次のような穴あきドーナッツのような天体に住んでいたらどうでしょうか。
矢印のような航路を通っても、確かに一周して戻ることができます。この 2 つの天体の形は、ビーチ ボールと浮き輪の違いと思うとわかり易いと思います。
私たちが巨大なビーチボールの上に住んでいる場合と、巨大な浮き輪の上に住んでいる場合とを想 像して下さい。どちらの場合も、自分の回りには平坦に見える地面と、青い空が見えるばかりで、自 分がビーチボールの上にいるのか、浮き輪の上にいるのかの区別はつきません。そこで、次のような 問題が生じます。
全体を見ることなく、全体を知る方法はないだろうか。
この問題に数学的な言葉と方法を与えたのが岡潔の不定域イデアルの理論または層の理論です。
地球の形を知ろうとする場合、さしあたり私たちができることといえば皆で協力して地図を作り、 それをつなぎ合わせてみることです。地図というのは先ほど紹介しました座標を考えるということと 同じです。地球上の各地の人たちがそれぞれ自分の回りに描ける座標を可能な限り求め、それらのつ なぎ方までわかれば、より多くの情報が得られ、地球全体の形についての詳細な情報がわかります。 例えば,皆が,もしまっすぐな座標をもつ地図を持ち寄って来たとしたら,地球は平面だということ になりますし,スイカの皮のように緩やかに湾曲した地図を持ち寄ってきたら,地球は球だというこ とになります.
しかし、各地点で描ける座標を「すべて」求めたり、隣との貼り合わせ方を「すべて」試すなどと いうことは、とうてい無理な作業です。この点が難問として数学者を悩まし、問題の解決を何十年も 遅らせました。岡潔は、この困難を乗り越えるために、必要な概念や道具をすべて 1 人で揃え、問題 を解決していったのでした。それが不定域イデアルの理論であり、層の理論です。
デカルトの発見した座標の理論が、すべての数学者に受け入れられ、それがさらに広く科学一般、 科学技術に浸透して行くのに数百年の時間を要しました。岡潔の理論は、今では数学者の知らぬ者は 無いほど浸透してきましたが、これがさらに科学一般に広まり、技術分野に応用を持つにはどれほど の時間がかかるかわかりません。数百年後には、岡の理論が高校で教えられる時代が来るかも知れま せん.それほど岡潔の発見は,長く歴史に残るものです.デカルトの座標の発見に匹敵する発見をし た岡潔は,20 世紀最大の数学者の一人と位置付けられる事になるでしょう。
http://www.edu.city.hashimoto.wakayama.jp/gakkyou/kouen.pdf
§5 …岡潔がどのような数学の発見をしたのか説明をいたします。…
それは一言で言うと、図形が与えられたとき、その部分的(局所的)なデータと、全体的(大域的) な
データとを結びつける数学的な言葉=概念を発明したことです。この理論を岡潔は不定域イデアル
の理論とよびましたが、今では層の理論と呼ばれています。
岡潔 - Wikipedia
http://ja.wikipedia.org/wiki/%E5%B2%A1%E6%BD%94
数学者としての挑戦[編集]
フランス留学時代に、生涯の研究テーマである多変数解析函数論に出会うことになる。当時まだまだ発展途上であった多変数解析函数論において大きな業績を残した。一変数複素関数論は現代数学の雛型であり、そこでは幾何、代数、解析が三位一体となった美しい理論が展開される。現代数学はこれを多次元化する試みであるということもできよう。解析の立場から眺めると一変数複素関数論の自然な一般化は多変数複素関数論であるが、多変数複素関数論には一変数の時にはなかったような本質的な困難がともなう。これらの困難を一人で乗り越えて荒野を開拓した人物こそ岡潔である。
具体的には三つの大問題の解決が有名だが、特に当時の重要な未解決問題であったハルトークスの逆問題(レヴィの問題ともいう。および関連する諸問題)に挑み、約二十年の歳月をかけてそれを(内分岐しない有限領域において)解決した。岡はその過程で不定域イデアルという概念を考案したが、アンリ・カルタンを始めとするフランスの数学者達がこのアイデアをもとに層という現代の数学において極めて重要な概念を定義した。また、(解析関数に関する)クザンの第2問題が解けるためには、それを連続関数の問題に置き換えた命題がとければよいとする「岡の原理」も著名である。
その強烈な異彩を放つ業績から、西欧の数学界ではそれがたった一人の数学者によるものとは当初信じられず、「岡潔」というのはニコラ・ブルバキのような数学者集団によるペンネームであろうと思われていた事もあるという[5]。
225 2/25(火)20:02 0
上空移行の原理(第一論文)(インスピレーション型)
二関数を積分方程式に帰着させ融合させる方法(第六論文)(梓弓型)
不定域イデアルの理論(第七論文)(情操型)
専門外から見てだが、一つ目の大発見は峻険な山脈を一から登るのを諦めてヘリコプターで登ることで得た発見。
二つ目の大発見は過去の積み重ねを切り捨てて知性を総動員して見つけ出した発見。
三つ目の大発見は牛乳に酸を入れた時のようにいちめんにあったものが固まりになって分かれたことでわかった発見。
特に三つ目は「捨」と「情」により結果としてまったく新しい概念を考案してしまったために、
その後の数学専門書の記述に革命をもたらしたと言って良い。
でも逸話としては第十論文の方が好きかな。厳しい寒さの冬から果実のなる春に移った、岡の最後の論文。
ブルバキ的な厳しさとは無縁の、おまけみたいな論文だから、相手にしない人も多いんだけどね。
掲載された図形の世界観が、第十論文だけは本当に異質で面白い。
長文書いてくれる人は次はこの岡の数学研究回顧・伝記をお願いしたい。
既刊に出てる奴でいいから。
Amazon.co.jp: 天才数学者たちが挑んだ最大の難問―フェルマーの最終定理が解けるまで (ハヤカワ文庫NF―数理を愉しむシリーズ): アミール・D. アクゼル, Amir D. Aczel, 吉永 良正: 本
によると,
ロシアのエカテリーナ二世が即位しオイラーを再びサンクト・ピーテルブルッツのアカデミーに招くと,彼は喜んで戻っていった.その頃,フランスの無神論者で哲学者のデニ・ディドロがエカテリーナの宮廷を訪れていた.女帝は神の存在についてディドロと論議するようオイラーに求めた.ディドロはこの有名な数学者が神の存在を証明したと聞かされていた.オイラーはディドロに近づくと,重々しい声でこう述べた.
「先生,a+b/n=x,ゆえに神は存在する.ご返答願いたい」ディドロは数学について何一つ知らなかったので反論もできず,ただちにフランスへ帰国した.
http://d.hatena.ne.jp/tullio/20080317/1205765600
http://blogs.yahoo.co.jp/yuugao3824/149745.html
ロシアの女王エカチェリーナ1世はフランスの哲学者デニ・ディドロに盛んに無神論を論じられ、辟易してオイラーと打ち合わせてディドロをロシアから追放しようとしました。
そこで宮廷のみんなの前でオイラーはディドロに、
「 (a+b^2)/n = x、ゆえに神は存在する。ご返答願いたい」
と言いました。
ディドロは数学について何1つ知らなかったので反論できずに大恥をかき、直ちにフランスへ帰国したそうです。
もしディドロが数学を知っていたら
「a = 1, b = 2, n = 3のときはx = 3になる。
a = 3, b = 3, n = 3のときはx = 10になる。
どうしてその前提から神が存在すると言えるのですか?」
と答えたことでしょう。
そう答えられたらオイラーは反論できなかったと思います。
オイラーはディドロが数学を知らないことをいいことに、数学を悪用したのでした。
さて、今日使われている数学用語の多くはオイラーが定めたものです。
有名なオイラーの公式 eiθ = cosθ + i sinθ にθ=πを代入すると、eiπ = -1になります。
これは起源の全く異なる重要な2つの自然定数、円周率π= 3.1415926535...とネイピア数e = 2.7182818284590...が数の体系の基礎である0と1、そして虚数単位iが足し算、掛け算、べき乗という3つの基本操作によって結ばれている非常に重要な等式です。
このため、オイラーの等式は「人類の至宝」とも呼ばれます。
オイラーはこれを愛し、最高の美と考えてアカデミーの門に掲げました。
また、オイラーは医学を含め、何を勉強していても数学を見出しました。
耳の生理学を勉強する中で、オイラーは波の伝播の数学的解析を考察しました。
参考文献 『天才数学者たちが挑んだ最大の難問』 アミール・D・アクゼル著 早川書房
『素顔の数学者たち』 片野善一郎著 裳華房
「 (a+b^n)/n = x、ゆえに神は存在する。ご返答願いたい」
正確には上記の式
nが再帰的なのがポイント
オイラーによる神の存在証明[編集]
18世紀の数学者レオンハルト・オイラーは、ロシアに滞在していた時、エカチェリーナ2世から「ディドロが無神論を吹聴しているので何とかしてほしい」という依頼をうけた。オイラーはディドロと対決し、
「閣下、 故に神は存在する。何かご意見は?」
と問いかけたところ、数学の素養のないディドロは尻尾をまいて逃げた、というエピソードが語られている。無論、この数式は何の意味もない全くのデタラメである。しかし実際のところ、ディドロは数学の教養が十分にあったことから、この逸話は単に見かけ倒しの学識でいかに相手を困惑させられるかという発想に当てられただけの可能性が高い[1]。
J.ファング、『ブルバキの思想』、森毅訳、東京図書、p.13。本書ではディドロが微分方程式の専門的な知識を要する論文を完璧に発表していたことから、この逸話の事実性を否定している。( ディドロが書いた数学に関する書物 )しかし、この逸話でオイラーが行ったような学術的はったりはしばしば見受けられ、近年ではデタラメな自然科学・数学用語を用いた論文を文芸評論雑誌が掲載してしまったソーカル事件などが有名である。
http://ja.wikipedia.org/wiki/神の存在証明#.E3.82.AA.E3.82.A4.E3.83.A9.E3.83.BC.E3.81.AB.E3.82.88.E3.82.8B.E7.A5.9E.E3.81.AE.E5.AD.98.E5.9C.A8.E8.A8.BC.E6.98.8E
神の存在証明 [日常]
「閣下、a+b^n/n = x
故に神は存在す。如何?」
Leonhard Euler
エカテリーナロシア女帝の前にて、Denis Diderotに対して。
--
(^nはn乗の意)
この人以外にはちょっと成立しえない格好良い証明。
あまり注目されないが、この言葉に敗北を認めたディドローもまた、只者ではありえないと思う(哲学者としての態度ではなく、真理に仕える人としてのそれにおいて)。
いくら「数学の素養がない」とは言え、「この数式が神の存在をどのように証明する?」などという月並みな反論をしなかったのだから。
ちなみに、a+b^n/n = x というのは、「オイラーがディドローをやりこめるために適当に言った何の意味もない数式」というのが一般的な見解。
でも、もしオイラーが a+b^n/n = x の代わりに e^iπ + 1 = 0 (πは円周率のパイ)と言っていたらどうだろう?
あるいは、ξ(2) = π^2/6 (ξはゼータ関数の意) なら?
たぶん、現代のほとんどの数学者は、「オイラーの言葉は真理である」と認めるんじゃないだろうか。
ディドローが屈したのは、a+b^n/n = x そのものではなく、a+b^n/n = x に象徴される、オイラーが積み上げ続けた神の存在証明に対してであったと思う。
神は細部に宿りたもう。
http://unterdenlinden.blog.so-net.ne.jp/2007-11-11
ベルヌーイ数
ベルヌーイ数 (ベルヌーイすう、Bernoulli number) は数論における基本的な係数を与える数列であり、もともと、連続する整数のべき乗和を定式化する際の展開係数として1713年にヤコブ・ベルヌーイが著書 Ars Conjectandi (推測術) にて導入した[1]ことからこの名称がついた。 ベルヌーイ数は、べき乗和の展開係数にとどまらず、級数展開の係数や剰余項、リーマンゼータ関数においても登場する。また、ベルヌーイ数はすべてが有理数である。
目次 [非表示]
1 定義
1.1 ベルヌーイ数の一般項
1.2 漸近的性質
2 ベルヌーイ数を用いた級数展開
3 べき乗和による導入
4 関連項目
5 脚注
定義[編集]
ベルヌーイ数 は下に示すマクローリン展開 (テイラー展開) の展開係数として定義される。
この定義から、関数 を繰り返し微分していけばベルヌーイ数を得ることができるが、そのような手段でベルヌーイ数を得るのは容易ではない。 ベルヌーイ数を計算するには、マクローリン展開ではなく、次の漸化式を用いる。この漸化式から、ベルヌーイ数がすべて有理数であることがわかる。
ここで、は二項係数 (二項定理 参照) である。 上の漸化式を用いて、ベルヌーイ数を第 29 項までを算出すると下表のようになる。 この表には、ベルヌーイ数が有理数であるので、分子と分母を記載している。
n 分子 分母 n 分子 分母 n 分子 分母
0 1 1 10 5 66 20 −174611 330
1 −1 2 11 0 — 21 0 —
2 1 6 12 −691 2 730 22 85 4513 138
3 0 — 13 0 — 23 0 —
4 −1 30 14 7 6 24 −236 364 091 2 730
5 0 — 15 0 — 25 0 —
6 1 42 16 −3 617 510 26 8 553 103 6
7 0 — 17 0 — 27 0 —
8 −1 30 18 43 867 798 28 −23 749 461 029 870
9 0 — 19 0 — 29 0 —
ベルヌーイ数の漸化式は、上記の関数 の逆数をテイラー展開し、その 2 つの積が 1 になることから導出できる。その漸化式は厳密な計算には有用であるが、 が大きくなると途中の式の値が非常に大きくなるため、浮動小数点数を使って計算する場合、精度が著しく悪くなる計算として知られている。
奇数番目のベルヌーイ数は 以外はすべて 0 であり、偶数番目は を除いて正の数と負の数が交互に並ぶ。 ベルヌーイ数の第 3 項以降の奇数項が 0 となることは、正接関数 (tangent) のマクローリン展開から証明[2]できる。
ベルヌーイ数の一般項[編集]
第 2 種スターリング数との関係 (スターリング数 参照) から、次のようなベルヌーイ数の一般項を算出する公式が存在する。
この公式は、総和記号が二重になっているため、上に示した漸化式ほど手軽にベルヌーイ数を計算する公式ではない。
漸近的性質[編集]
ベルヌーイ数とリーマンゼータ関数の関係から、ベルヌーイ数に次の漸近的性質があることが導かれる。
ベルヌーイ数を用いた級数展開[編集]
ベルヌーイ数は、いくつかの双曲線関数と三角関数の級数展開における展開係数となる。 ベルヌーイ数を展開係数とする関数とそのローラン級数による表現を挙げる。 まず、余接関数 (cotangent) のローラン級数展開は次のようになる。
第 1 の関係式は、ベルヌーイ数が の展開係数であることを利用して数式変形すれば得られる。 第 2 の関係式は であることを利用すれば、第 1 の関係式から導き出される。これらの級数の収束半径は である。 次に正接関数 (tangent) のローラン級数展開は次のようになる。
この関係式は、 を利用して余接関数のローラン級数展開を変形すれば導出できる。 なお、この級数の収束半径は である。 この正接関数のローラン級数展開の展開係数による数列はタンジェント数と呼ばれる。 一方、余割関数 (cosecant) は次のようにローラン級数展開される。
この関係式は、 を利用すれば導出できる。 なお、この級数の収束半径は である。
べき乗和による導入[編集]
ベルヌーイ数は、もともと、連続する整数のべき乗和を定式化する際に、展開係数として導入された。 現代の表記法によって書くならば、定式化するべき乗和とは、
なる級数である。この級数は、ベルヌーイ数を用いて、
のように書くことができる。 ベルヌーイ数の漸化式は、べき乗和を定式化した際の考察から得られる。 さらに、ベルヌーイ数の指数型母関数 (母関数 参照) が となることから、その母関数を現在ではベルヌーイ数の定義とする。
ヤコブ・ベルヌーイは彼の著書『推測術』でベルヌーイ数を導入した際、べき乗和を上に書いたような から にわたる和でなく、 から にわたる和:
として扱っていた。 ベルヌーイは、その著書で整数のべき乗 の和を計算する公式として、次の数式を記している[3]。
この数式に記載されている展開係数 がベルヌーイ数 ( 以降) である。ベルヌーイが記した数式は、
に相当する。この数式に用いた展開係数 は、
のように、 においてベルヌーイ数と一致する。一部の文献[4][5]では の代わりに をベルヌーイ数と呼んでいる。
一方、日本ではベルヌーイとほぼ同時期に関孝和がべき乗和を定式化し、ベルヌーイ数を発見していた[6]。 そのため、ベルヌーイ数を関・ベルヌーイ数と書いている文献[7]もある。
関連項目[編集]
ヤコブ・ベルヌーイ
関孝和
ファウルハーバーの公式
ベルヌーイ多項式(英語版)
ゼータ関数
三角関数
脚注[編集]
[ヘルプ]
^ Julian Havil, "オイラーの定数 ガンマ," 新妻弘 訳, 共立出版, 初版, pp.97-99, 2009.
^ 正接関数のマクローリン展開の結果において、実数変数を仮定した場合、ベルヌーイ数の第 3 項以降の奇数項は虚数項に対応する。 実数変数における正接関数が実数関数でなければならないので、そのマクローリン展開に虚数項に対応する項が存在してはならない。 よって、ベルヌーイ数の第3項以降の奇数項はゼロでなければならない。
^ E. Hairer, G. Wanner, "解析教程 上," 蟹江幸博 訳, シュプリンガー・ジャパン, 新装版, p.18, 2006.
^ 例えば、 荒木恒男, 伊吹山知義, 金子昌信, "ベルヌーイ数とゼータ関数," 牧野書店, 2001.
^ Wikipedia ファウルハーバーの公式 もベルヌーイの記述に基づき、第 1 項を1/2とする記述で説明している。
^ 小川束, "関孝和によるベルヌーイ数の発見," 数理解析研究所講究録, 第1583巻, 2008.
^ 例えば、 桜井進, 中村義作, "天才たちが愛した美しい数式," PHP研究所, 第1版, p.205, 2008.
カテゴリ: 数論有理数数学に関する記事
ベルヌーイ数
みなさんは、自然数のべき乗和を計算したことはありますか? たとえば、n個の自然数の1,2,3,...,6乗和は次のようになります。
ヤコブ・ベルヌーイは1713年に ベルヌーイ数を発表しました。それは次のような数字です。
ベルヌーイ数
n Bn
0 1
1 1/2
2 1/6
3 0
4 -1/30
5 0
6 1/42
n個の自然数の1,2,3,...,6乗和は ベルヌーイ数で次のように表現できます。
ベルヌーイ数の定義には2種類あります。 ベルヌーイ多項式を Bn (x ) としたとき、 次の2種類です。
Bn = Bn (0)
Bn = Bn (1)
本ページでは、 後に説明するベルヌーイ関数の定義と合わせるため、 後者の定義を採用します。
http://www.geocities.jp/x_seek/zeta.html
http://www.komaba-s.tsukuba.ac.jp/ssh/library/126.htm
カントール集合
カントール集合は以下のようにしてつくられる自己相似的な集合である.最初に長さ1の線分を用意し,3等分する.コッホ曲線のときは真ん中の部分を出っ張らせたが,こんどは真ん中の部分を取り去ってしまう.すると2本の線分ができるから,それぞれ3等分して同様な作業を行う.これを無限回繰り返し行ってできる図形がカントール集合である. 1回の作業で図形の長さは2/3になるから,無限回の作業ののちにできるカン トール集合の長さは0である.フラクタル次元を計算することもできる.カントール集合は,自分自身を1/3に縮小したものが2個できるように分けられるから,フラクタル次元はlog_3 2(<1)である.カントール集合は,3進法で小数に表したときに2と0のみで表されるような数全体になっている.例えば,3進法で0.022202022…という数はカントール集合に入っているが,この数に,小数表示の2を1に変えて,2進小数と思った数0.011101011…を対応させることを考えよう.他の数も同様に対応させることによって,カントール集合の点と0以上1以下の点との1対1対応をつくることができる.このことから,カントール集合は不可算無限個の点の集合であることがわかる.
_______________________
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| |___________|
| | | |
| | | |
| | | |
| | |_____|
| | | | |
| | | |__|
| | | | |
|___________|_____|__|__|
無限級数の活用
無限級数
1+1/2+1/4+1/8+…+1/2^(n-1)…
の収束・発散を調べ、収束するときは和を求めよ。
第 n 部分和 Sn=1+1/2+1/4+・・・+1/2n-1=2(1-(1/2)n) なので、
数列 { Sn } は収束し、n → ∞ のとき、Sn → 2 である。
したがって、無限級数は収束し、その和は、2 である。
(注意) Sn+1/2n-1 を順次計算して、Sn+1/2n-1=2 を示してもよい。
上記のことは、次のように図式化すれば、極限の計算を知らなくても納得できるだろう。
____________________________________________
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| |______________________|
| | | |
| | | |
| | | |
| | |___________|
| | | | |
| | | |_____|
| | | | | |
|_____________________|__________|_____|__|__|
上記の無限級数は、無限等比級数(幾何級数)といわれる。
http://www004.upp.so-net.ne.jp/s_honma/series/series.htm
無限級数の活用
情報理論wiki
歴史的背景[編集]
1948年6月と10月、クロード・シャノンは Bell System Technical Journal 誌で古典的論文 "A Mathematical Theory of Communication" を発表し、情報理論を学問分野として確立し、世界的な注目を浴びた。
この論文以前、ベル研究所で考えられていた情報の理論は限定的であり、あらゆる事象が同じ確率で発生することを暗黙の前提としていた。1924年、ハリー・ナイキストの論文 Certain Factors Affecting Telegraph Speed(テレグラフの速度を制限する要因)では、通信システムにおける「情報; intelligence」と「回線速度」の定量化に関する理論が述べられている。それによると、情報の転送速度 W は で表され、m は選択可能な電圧レベル数、K はある定数である。1928年、ラルフ・ハートレーの論文 Transmission of Information(情報の伝送)では、測定可能な量として「情報; information」という用語が使われている。その中で情報の定量化は で表され、S は文字の種類数、n は伝送された文字数であるとした。後に十進の情報量を表す単位をハートレー(Hartまたはhartley)と呼ぶようになった。1940年、アラン・チューリングは、第二次世界大戦時のドイツ軍の暗号統計解析の一部として同様の考え方を使った。
確率の異なる事象群を扱う情報理論の基礎となる数学は、ルートヴィッヒ・ボルツマンとウィラード・ギブスによる統計力学からもたらされた。情報理論におけるエントロピーと熱力学におけるエントロピーは単なる用語の類似以上の関連がある(ランダウアーの原理参照)。
シャノンの革新的論文については、ベル研究所での研究で1944年末ごろには実際の研究はほとんど済んでいた。シャノンの理論は情報理論の基礎となる静的プロセスとしての通信のモデルを提案し、論文冒頭で次のように表明している。
「通信の基本的課題は、ある地点で選択されたメッセージを正確または近似的に別の地点で再生することである」
それと共に次のような概念が提唱された。
情報源の情報エントロピー、冗長性、情報源符号化
ノイズのある伝送路での伝達情報量、伝送路容量、伝送路符号化
シャノン=ハートレーの定理の応用としてのガウスノイズのある伝送路での伝送路容量
情報の基本単位であるビット
ゼノンのパラドックス
曖昧さ回避 「アキレスと亀」はこの項目へ転送されています。北野武の映画作品については「アキレスと亀 (映画)」をご覧ください。
ゼノンのパラドックスは、エレア派のゼノンの考えたパラドックスで、パルメニデスの「感覚は全て疑わしいものである」こと、特に「一があるのであって多があるのではない、多があるとすれば運動は不可能である」という学説をピタゴラス学派の多を主張する立場を批判して唱えたものであった。
今日、ゼノンのパラドックスと呼ばれるものは、アリストテレスの『自然学』と、それについてキリキアのシンプリキオス(英語版)が著した注釈との中に8つ伝わっている。そのうちのいくつかは、本質的に同じ問題を取り扱ったものである。
目次 [非表示]
1 パラドックスの概要
1.1 二分法
1.2 アキレスと亀
1.3 飛んでいる矢は止まっている
1.4 競技場
2 数学的な解釈
3 哲学的な観点から
4 思想史
5 その他
6 参考文献
7 注釈
8 関連項目
9 外部リンク
パラドックスの概要[編集]
ゼノンの論証がパラドクシカルである所以は「それらが導く結論はいかにも非現実的であるにもかかわらず、結論を導く論証過程自体は正しそうに見える」点にある。つまり論証の前提の正しさを受け入れる者にとって、論証の結論を拒否するためには論証過程のどこに誤りが潜んでいるかを指摘する必要があるが、それは容易ではない。結果として後に多くの哲学者がこの課題に挑戦した。
ただしゼノンの意図としては、これらの論証によってその非現実的な結論を主張したかったわけではない。「世界が不可分な要素的な点やアトムからなる」という前提から「運動が不可能となる」という帰結を導き出すことで、運動が可能であるという現実との矛盾を示そうとした、一種の背理法である。その場合「運動自体を否定しよう」というつもりはそもそもゼノンにはなく「否定されるべきはむしろ、そのような非現実的な結論を導く際に前提としてはたらいていた考え方にある」というのがゼノンの考えであった。
以下、ゼノンが提示したとされるパラドックスのうち「運動のパラドックス」としてアリストテレス『自然学』[1]が伝える4つを掲げる。
二分法[編集]
地点Aから地点B0へ移動するためには、まずAからの距離がAB0間の距離の半分の地点B1に到達しなければならない。さらにAからB1へ移動するためには、Aからの距離がAB1間の距離の半分の地点B2に到達しなければならない。以下、同様に考えると、地点Aから地点B0へ移動するには無限の点を通過しなければならず、そのためには無限の時間が必要である。よって、有限の時間で地点Aから地点B0へ移動することは不可能である。
アキレスと亀[編集]
「走ることの最も遅いものですら最も速いものによって決して追い着かれないであろう。なぜなら、追うものは、追い着く以前に、逃げるものが走りはじめた点に着かなければならず、したがって、より遅いものは常にいくらかずつ先んじていなければならないからである、という議論である。」アリストテレス『自然学』
あるところにアキレスと亀がいて、2人は徒競走をすることとなった。しかしアキレスの方が足が速いのは明らか[2]なので亀がハンディキャップをもらって、いくらか進んだ地点(地点Aとする)からスタートすることとなった。
スタート後、アキレスが地点Aに達した時には、亀はアキレスがそこに達するまでの時間分だけ先に進んでいる(地点B)。アキレスが今度は地点Bに達したときには、亀はまたその時間分だけ先へ進む(地点C)。同様にアキレスが地点Cの時には、亀はさらにその先にいることになる。この考えはいくらでも続けることができ、結果、いつまでたってもアキレスは亀に追いつけない。
ゼノンのパラドックスの中でも最もよく知られたものの一つであり、多数の文献は彼の手に帰しているが、歴史家パボリノスの説によれば、この議論を創始したのはパルメニデスであるという[3]。
その議論やキャラクターの面白さから、アキレスと亀という組み合わせは、この論自体とともに多くの作家に引用された。たとえば、ルイス・キャロルの『亀がアキレスに言ったこと』や、ダグラス・ホフスタッターの啓蒙書『ゲーデル、エッシャー、バッハ』に主役として登場する。
飛んでいる矢は止まっている[編集]
「もしどんなものもそれ自身と等しいものに対応しているときには常に静止しており、移動するものは今において常にそれ自身と等しいものに対応しているならば、移動する矢は動かない、とかれは言うのである。」アリストテレス『自然学』
アリストテレスは続けて、「この議論は、時間が今から成ると仮定することから生ずる」と述べている。この言から、ゼノンも「時間が瞬間より成る」を前提としていると解される。瞬間においては矢は静止している。どの瞬間においてもそうである。という事は位置を変える瞬間はないのだから、矢は位置を変えることはなく、そこに静止したままである。ゼノンの意が単純にこうであったのかは確定的な事ではない。
競技場[編集]
競技場において、一瞬の間に1単位の距離を移動することができる2台の馬車を考える。
▲▲▲▲ 観客席
□□□□ 馬車・・・移動方向は右(→)
■■■■ 馬車・・・移動方向は左(←)
それぞれの馬車が移動を開始し、次のように客席に対して1単位だけ移動したとする。
▲▲▲▲
□□□□
■■■■
このとき、いずれかの馬車に対してもう一方の馬車がどれだけ移動したかを観察すると、2単位移動している。すなわち「馬車は一瞬のうちに1単位移動しようとすれば2単位移動しなければならない」ことになり、これは不可能である。したがって馬車の運動は不可能である。
数学的な解釈[編集]
「アキレスと亀」は、二つの条件(亀がアキレスの前からスタートする、亀はアキレスより遅い)の下において、追付くか否かが問題とされている。純粋に数学的に見れば、この条件下では、それは定まらない。ゼノン式に捉えたとしてもそれは同じである。従って、ゼノンの誤りは、何れとも決せられないことであるのに、一方を断じていることである。そのことは、アリストテレスを始めとする、ゼノン式の捉え方そのものが問題を孕むのだとする論議は、追付かないケースもある事を見ていない限りにおいて、何処かに問題を孕んでいる可能性があることを示唆している。
追付かないケースは、亀がアキレスより遅い事を維持しつつ、両者の速度差が急速に縮まる設定にすれば作ることが出来る。無数に作り得るが、古代ギリシャ時代の数学では困難であったかも知れない。
両者が等速で動くと仮定するならば、以下のように、ゼノン式捉え方で、追付くことを示すことが出来る。
アキレスの走行速度を v m/s、亀の歩行速度を rv m/s とし、亀はアキレスより L m 前方にいるとする(亀の歩行速度はアキレスの走行速度よりも小さいので、 0<r<1 である)。両者が同時にスタートして、アキレスが亀の出発点まで到達する時間は \frac{L}{v} s である。その時亀はアキレスより rv\times\frac{L}{v}=rL m 前方にいる。そしてアキレスがその位置まで到達するのはさらに \frac{rL}{v} s 後であり、その時亀はさらに r^2L m 前方に存在する。以下同様にそれを繰り返していくと、アキレスが亀の位置まで到達する時間の合計は
\frac{L}{v}+r^1\frac{L}{v}+r^2\frac{L}{v}+r^3\frac{L}{v}+\cdots
となる。つまり、項が無限に続き、「常にいくらかずつ先んじて」いるかに見える。
だが、項が無限にあっても、「常に」即ち「時間の無限」においてではない。これは初項 \frac{L}{v} 公比 r の等比数列で、 n+1 項までの和は
\frac{L}{v}+r^1\frac{L}{v}+r^2\frac{L}{v}+r^3\frac{L}{v}+\cdots+r^n\frac{L}{v}= \frac{(1-r^{n+1})\frac{L}{v}}{1-r}
となる。ここで n が無限大であるとすると、0<r<1 であるので r^{n+1} は0となる。つまり
\frac{L}{v}+r^1\frac{L}{v}+r^2\frac{L}{v}+r^3\frac{L}{v}+\cdots
と無限に加算した場合の総和は \frac{\frac{L}{v}}{1-r} s となる。このように級数の収束の問題に還元される。
なお、最後の計算結果は、パラドックスのことを忘れて「アキレスがt秒後に追いつく」として立てられる1次方程式
vt=L+rvt
の解と一致している。
「飛んでいる矢は止まっている」では、アリストテレスは、時間が「不可分割的な今から成るのではない」としてゼノンを否定する一方、「今においては運動も静止もありえない」(第6巻第8章)として、疑似的な論議と見ている風もある。数学的に見れば、瞬間においては運動も静止もないと見ることも可能であるが、同時に、運動方程式は瞬間における速度を示し得るのであって、言葉の定義の問題に過ぎない。しかし、前者の否定は成り立たない。時間が瞬間より成るとしても、運動は否定され得ない。時間が連続体であれば、時間が瞬間=点よりなり、矢が瞬間=点においては静止しているとしたとしても、動くことは出来る。近代解析学においては、ゼノンの結論は否定されるが、アリストテレスの論議も否定される。
哲学的な観点から[編集]
哲学的には、数学的な前提に立った場合のように、このパラドックスは「間違っている」とは見なされない。極限や収束をどう理解するかと、特に「仮に有限を無限の回数の加算の結果と『見なしうる』ということから、現にそうした無限個の『加算されたもの』から『構成されている』と言っていいかどうか」が、このパラドックスでは問題になる。
つまり確かにパラドックスの結論は不合理なもののように見えるが、それは「不連続な複数の単位から構成される連続という(原子論者の考えたような『多』の)立場を前提にすると不条理に陥る、ゆえにこの『多』という仮定が間違っており、連続は『一』が基底的な属性であって、より基底的な『多』から「一」が構成されているとはいえない」という背理法の論法なのである。
それが「無限に切り分けられる」ことと「無限に足し合わせられたものからなっている」ことは、一見同じことのように見えるが違う。そして現実の運動や連続について、前者は言えるが、後者はいえない。
「線を無限に分割して、無限にたくさんの点を見い出せる」ことから「線が無限にたくさんの点からなっている」とは言えない。ゼノンやエレア派的にいえば、無をいくら足しても有にはならない。有がある以上、どこかに有の起源が無ければならない。長さゼロの点から長さ一の線を作る事は出来ない。ゼロをいくら加算しても一にはならない。しかし線と線の交点として点を定義する事は出来る。
これは不動の矢のパラドックスにおいてより根本的に現れており、いわゆるこの動かない動く矢は、あくまでも運動の或る瞬間の概念的切片であって、現実に特定の瞬間に特定の位置を占めているそうした要素的断片が実在的に「存在」し、その加算として運動があるわけではない。連続がまずあって、それを切片に切って把握することができるのであって、要素的な断片がまずあって、それが合わさって連続が構成されているのではない。(ピュタゴラス派的「数字」や「点」の議論)運動という連続は「多」からなっているわけではない。
さらにいえば「パラパラマンガやアニメのようなものとして、現実の連続性を理解することはできない」ことが、このパラドックスの、そしてエレア派の問題にしていることなのである。
思想史[編集]
アリストテレスは「無限にあるものが現勢的でなく可能的にあるのだとすれば、それらを通過し尽くすことは可能である」としている。
レオナルド・ダ・ヴィンチは、「点とはありうるかぎりのものよりさらに小さいものであり、線はその点の運動によって作られる。線の極限は点である。次に面は線の運動から生れ、そしてその極限は線である。立体は(面積の)運動によって作られる。(そしてその極限は面である)(「手記」)」と語っている。
バールーフ・デ・スピノザは「持続が瞬間から成るとの主張は、悟性によって把握される不可分な無限の量、表象能力によって把握される可分的な有限の量の両者が区別されないことに基づく」と指摘している。
ゲオルク・ヴィルヘルム・フリードリヒ・ヘーゲルはゼノンの議論を認めた上で、そこから帰結するのは、運動が存在しないということでなく、運動は定有する矛盾であるということであるとしている。
アンリ・ベルクソンは、ゼノンの議論は時間や運動を空間に翻訳するものとした上で、運動そのものは持続であって分割不能であるとしている。
その他[編集]
量子力学では、放射性崩壊を起こす可能性のあるはずの不安定な原子核は、完全に連続した観測の下では崩壊を起こさない。このことは(ゼノンの議論と直接の関係はないものの)量子ゼノン効果と呼ばれている。
参考文献[編集]
中村秀吉(1980)『時間のパラドックス』(中公新書)
注釈[編集]
^ アリストテレス全集3『自然学』第6巻第9章、訳・出 隆、 岩崎 允胤、岩波書店刊: ISBN-13: 978-4000912839
^ イリアスにおいてアキレスの枕詞の一つは「駿足の」である
^ ディオゲネス・ラエルティオス 『ギリシア哲学者列伝(下)』 加来彰俊訳、岩波書店、1994年、110, 117。ISBN 4-00-336633-6。
関連項目[編集]
亀がアキレスに言ったこと - 「ゼノンのパラドックス」を引き継いだルイス・キャロルによるパラドックス
1/2 + 1/4 + 1/8 + 1/16 + ⋯ - 二分法を説明するのに用いられる数式
外部リンク[編集]
「Zeno's Paradoxes」 - スタンフォード哲学百科事典にある「ゼノンのパラドックス」についての項目。(英語)
http://w3.kcua.ac.jp/~fujiwara/infosci/bitbyte.html
ビット
2進数で表した数字のならび,またはその桁数のことをビットという。 bit は,2進数 binary digit からつくられた造語だ。 「少し」を意味する bit との掛詞か?
たとえばつぎのような2進数 00110101 は 10進数の
128×0+64×0+32×1+16×1+8×0+4×1+2×0+1×1=53
を表す。
ビットのならび 0 0 1 1 0 1 0 1
意味 128 64 32 16 8 4 2 1
4ビットのデータ(4桁の2進数)は 0~15 までの16通りの数字を表すことができる(24=16)。 同様に,8ビットのデータ(8桁の2進数)は 0~255 までの256通りの数字を表すことができる(28=256)。
シャノンの情報理論入門 価値ある情報を高速に、正確に送る (ブルーバックス) [Kindle版]
高岡詠子 (著)
1024この情報を表すには10このスイッチが必要
31頁
1024→512→256→128→64→32→16→8→4→2→1
数学には二種類ある
解析と離散
解析は全てを一つの数式に落とし込む一元論(収束しなければ二元論)で
離散はアナーキーな多元論
グラフ理論が後者の代表例
確率やトポロジーは両者を繋ぐ試み
マルクスは微分研究ノートを書いていたがその思考は解析寄りだ
彼の再生産表式も個別資本を捨象する方向にある
抽象能力が悪いわけではない
抽象出来ない現実、複数のノードがあることを知るべきだ、ということ
━━━━━━┓
┃
┃
┃
┃
┃
━━━━━━┛
┏━━━━┓
┃ ┃ ┃
┗━┛ ┏━┛
┃
┏━┓ ┗━┓
┃ ┃ ┃
┗━━━━┛
┓┏━┓┏━┓
┏┛┗┓┗┛┏┛
┃┏┓┃┏┓┗┓
┗┛┗┛┃┗━┛
┏┓┏┓┃┏━┓
┃┗┛┃┗┛┏┛
┗┓┏┛┏┓┗┓
┛┗━┛┗━┛
┏━┓┏━┓┏━┓┏━┓┏━┓
┗┛┏┛┗┓┗┛┏┛┗┓┗┛┏┛
┏┓┗┓┏┛┏┓┃┏┓┃┏┓┗┓
┃┗━┛┗━┛┃┗┛┗┛┃┗━┛
┗┓┏━━┓┏┛┏┓┏┓┃┏━┓
┏┛┗┓┏┛┗┓┃┗┛┃┗┛┏┛
┃┏┓┃┃┏┓┃┗┓┏┛┏┓┗┓
┗┛┗┛┗┛┗┛┏┛┗━┛┗━┛
┏┓┏┓┏┓┏┓┗┓┏━┓┏━┓
┃┗┛┃┃┗┛┃┏┛┗┓┗┛┏┛
┗┓┏┛┗┓┏┛┃┏┓┃┏┓┗┓
┏┛┗━━┛┗┓┗┛┗┛┃┗━┛
┃┏━┓┏━┓┃┏┓┏┓┃┏━┓
┗┛┏┛┗┓┗┛┃┗┛┃┗┛┏┛
┏┓┗┓┏┛┏┓┗┓┏┛┏┓┗┓
┗━┛┗━┛┗━┛┗━┛┗━┛
上の図はペアノ(Peano)曲線と呼ばれるもので、下の図の左のように、最初の単純な
曲線を半分に
縮小し、向きを変えて4枚貼り合わせます。
次に線で結びます。これを繰り返すとどんどん複雑になって無限に繰り返すと正方形を
埋め尽くします。
自己相似形の繰り返しという意味でフラクタルになっています。
フラクタルの例 ペアノ曲線のつくり方
図の右側のように4枚張り合わせるときに少し隙間を空ける(半分ではなく隙間分
考えて縮小しておく)
と下のようになりフラクタルらしいフラクタル図形になります。
http://yojiseki.exblog.jp/16238941/
"Sokkuri House" refrain only
http://youtu.be/4hJTm8pTV5A
「そっくりハウス」=宇宙際Teichmuller理論?
ABC予想を証明したと報道された数学者の望月新一氏は、自身のHPでその理論( 宇宙際Teichmuller理論、Inter-universal Teichmuller Theory)を説明する際に、谷山浩子「そっくりハウス」のアニメ(制作:山田塔子)を使っていた。
(整数問題やABC予想自体はスパイラル状の図解で説明するのが一般的らしいが↓)
When arranging the natural numbers in a spiral and emphasizing the prime numbers, an intriguing and not fully explained pattern is observed, called the Ulam spiral.
NHKみんなのうたで放送されたそのアニメは現在youtube及びニコ生から削除されてしまっている(エイベックスが販売したDVDが中古で入手可能だ)。
残念ながらその動画は紹介できないが、、、自分はこの映画を思い出した(入れ子状ではないが)。
OFFRET (The Sacrifice) [1986]
http://www.youtube.com/watch?v=k4izcNMy4rY
参考(論文):
(窓)http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal%20Teichmuller%20Theory%20I.pdf
(窓)http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal%20Teichmuller%20Theory%20II.pdf
(窓)http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal%20Teichmuller%20Theory%20III.pdf
(窓)http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal%20Teichmuller%20Theory%20IV.pdf
___________________
望月新一の過去と現在の研究
(窓)http://www.kurims.kyoto-u.ac.jp/~motizuki/research-japanese.html
「IUTeich理論って何?」...「そっくりアニメ」による解説
(窓)http://www.kurims.kyoto-u.ac.jp/~motizuki/sokkuri-hausu-link-japanese.pdf
宇宙際Teichmuller理論の出発点は、
入れ子になっている宇宙の列
というイメージにある。このようなイメージは、古代に遡るものと思われ、本稿で取り上げる「そっくりハウス」
のアニメをはじめ、世界各地の様々な物語・神話に登場するものである。宇宙際Teichmuller理論(IUTeich)
の場合、それぞれの宇宙は、
通常の環論・スキーム論が有効な古典的数論幾何的舞台一式
に対応する。アニメの中では、この宇宙たちは「家」という形で表される。それぞれの古典的数論幾何的舞台
の中にテータ関数があるが、このテータ関数は、 「次の宇宙」との間の「フロベニオイド論的」 (=非スキーム
論的!Frobenioids I, II及び´ Etale Thetaを参照) 「橋渡し役」を果たすのである。アニメでは、このリンク役の
テータ関数に対応するものは、 「小さな家」の中を覗き込む少女の目線
である。実際、少女の大きな目はテータ Θ のような形をしているように見えなくもない(笑) ! IUTeichでは、
ガロア群や数論的基本群 は、それぞれの宇宙の間を、膨張・圧縮されることなく同型なまま自由に往来できる
「不思議な物質」で出来ている。アニメでは、この「不思議な物質」に対応するものは、 「小さい家」 ・ 「大きい家」
の間をつなぐ「不思議な星たち」である。この
「クルクル回る星たち」の回転
は、IUTeich では、フロベニオイドの理論(Frobenioids I, II)における「エタール型物質」の性質を表しているものと
見ることもでき、またTopics IIIのモノ遠アーベル理論における「足し算と掛け算の回転」に対応しているものと見る
こともできる。IUTeichの最も深くかつ最も激しい部分は、この
Topics III のモノ遠アーベル理論や、エタール・テータ関数の様々な剛性性質
(後者については、´ Etale Thetaを参照)によって構成される、入れ子宇宙の列に対する標準的な分裂である。
この標準的な分裂は、pTeich(=p進Teichm¨ uller理論)における標準的な持ち上げ、あるいはもっと初等的な
理論では、Witt環のTeichm¨ uller代表元に対応している。 (因みに、p進の理論では、IUTeichのそれぞれの
「宇宙」は、個々の部分商 ‘pn/pn+1’ の正標数的代数幾何に対応する。 )
______________
Twitterでの評判:
Nebutan @Nebutan
証明に使われている「新たな数学的手法」の一部、「宇宙際Teichmuller理論」の望月教授
による解説に「そっくりハウス」アニメが!
(窓)http://www.kurims.kyoto-u.ac.jp/~motizuki/sokkuri-hausu-link-japanese.pdf
しかし意味分からん/数学界最大の難問「ABC予想」解明か
(窓)http://www.nikkansports.com/general/news/f-gn-tp0-20120918-1019282.html
about 11 hours ago
@taniyama_ 『そっくりハウス』リクエストしました。新宿・青山では初めてです。ありがとうございました。もしかしたら望月氏は京都のライブに来ておられたりするのかな?
Twitterfurukitakeshi(ふるき)-4時間前
お気に入り|リツイート|返信
Choreograph Blog » Blog Archive » そっくりハウス ow.ly/dPqro 宇宙際Teichmuller理論。なるほどわからない。
Twitterbrzbb01(ろきせ)-7時間前
お気に入り|リツイート|返信
そっくりハウス聴いたことないからなあまだ。
NHKみんなのうたサイト:
http://cgi2.nhk.or.jp/minna/search/index.cgi?id=MIN200210_02
http://avexnet.jp/id/anhkm/discography/product/AVBA-14794.html
「IUTeich理論って何?」...「そっくりアニメ」による解説
http://www.kurims.kyoto-u.ac.jp/~motizuki/sokkuri-hausu-link-japanese.pdf
宇宙際Teichmuller理論の出発点は、入れ子になっている宇宙の列というイメージにある。このよう
なイメージは、古代に遡るものと思われ、本稿で取り上げる「そっくりハウス」のアニメをはじめ、
世界各地の様々な物語・神話に登場するものである。宇宙際Teichmuller理論(IUTeich)
の場合、それぞれの宇宙は、通常の環論・スキーム論が有効な古典的数論幾何的舞台一式
に対応する。アニメの中では、この宇宙たちは「家」という形で表される。それぞれの
古典的数論幾何的舞台の中にテータ関数があるが、このテータ関数は、 「次の宇宙」と
の間の「フロベニオイド論的」 (=非スキーム論的!Frobenioids I, II及び´ Etale Thetaを
参照) 「橋渡し役」を果たすのである。アニメでは、このリンク役のテータ関数に対応
するものは、 「小さな家」の中を覗き込む少女の目線である。実際、少女の大きな目は
テータ Θ のような形をしているように見えなくもない(笑) ! IUTeichでは、
ガロア群や数論的基本群 は、それぞれの宇宙の間を、膨張・圧縮されることなく同型なまま
自由に往来できる「不思議な物質」で出来ている。アニメでは、この「不思議な物質」に対応
するものは、 「小さい家」 ・ 「大きい家」の間をつなぐ「不思議な星たち」である。…
http://youtu.be/4hJTm8pTV5A
対角線論法も、ホテルの住人に例えられるそれぞれの数字は
ヒュームのように一対一対応を守るだけで全体が統制的に展開することを現している
人間が神を知らずに時に美しいものを生み出すように
対角線論法において、ホテルの住人にも例えられるそれぞれの数字は
ヒュームのように一対一対応を守るだけで全体が統制的に展開する
神を知らない人間が時に神々しいまでに美しいものを生み出すように
図形数
正方形に対応する四角数
図形数(ずけいすう、figurate numbers)とは、一定の規則で図形状に並べられた点の個数として表される自然数の総称である。その歴史は、古代ギリシアのピタゴラス学派が「万物は数である」との思想のもと、図形と数を結び付けたところにまで遡る。例えば、図形として正方形を考えると、数としては平方数を得る。平方数を図形数として見るときには、これを特に「四角数」と呼ぶ。
目次
用語
歴史
グノモン
脚注
参考文献
関連項目
外部リンク
用語編集
「図形数」に対応する英語は figurate number, figured number, figural number があるが、その意味する範囲は日本語、英語ともに曖昧さがある。古代ギリシアで扱われたもののみを指すこともあれば、4次元以上の図形に対応するものまで含める場合もある[1]。figurate number の訳語として「装飾数」が用いられた例もある[2]。
歴史編集
四角数は奇数の和と捉えられる。例えば、図は 42 = 1 (赤) + 3 (黄) + 5 (緑) + 7 (青) を意味する。
紀元前6世紀頃のピタゴラス学派は、三角数や四角数を用いて、いくつかの数の性質を導いたとされる。例えば、正方形状に並んだ点から次に大きな正方形を作るにはL字形の「部品」を付加すればよいことから、最初の n 個の奇数の和が n 番目の四角数であることが分かる。現代的な記法では
ということである。この性質を用いて、無数にピタゴラス数を得ることもピタゴラスは知っていた[3]。また、三角数の2倍が矩形数であることから、1 から n までの和の公式
を得る。
このように、図を用いることによって、様々な数の性質が確かめられる。例えば、連続する三角数の和は四角数である。現代的な式では
と表せる。やや複雑な例として、プルタルコスが記してディオファントスが引用したところによると、三角数の8倍に1を加えれば四角数となる。すなわち、
である[4]。
三角数の2倍は矩形数
連続する三角数の和は四角数
三角数の8倍に1を加えると四角数
紀元前2世紀のヒュプシクレス(英語版)は、三角数や四角数を一般化した多角数を定義した[5]。その後、スミュルナのテオン、ニコマコス(英語版)、イアムブリコス(英語版)らが多角数について論じた[4]。
正四面体に対応する四面体数
2世紀頃のニコマコスは、その著書『算術入門(英語版)』において、多角数は等差数列の和として定義されることを指摘したのみならず、種々の立体数についても述べている。具体的には、四面体数、四角錐数などの多角錐数、立方体数、切頂(英語版)多角錐数などである[6]。それよりも前に、紀元前4世紀頃のオプスのフィリポ(英語版)やスピューシップス(英語版)が四面体数について考察したと考えられるが、文献は残っていない[7]。
1544年、マイケル・シュティーフェル(英語版)は、三角数、四面体数に続く五胞体数などの、高次元版の図形数を定義した[8]。
近世ヨーロッパの数学者、バシェ(英語版)、フェルマー、オイラーらも多角数について論じている[9]。初等的な性質のみならず、フェルマーが多角数定理を予想し、オイラーが五角数定理を示すなど、やや高度な数論にも図形数は現れる。
1996年に出版されたコンウェイとガイ(英語版)の『数の本』には、その他のさまざまな図形数、例えば中心つき四角数や体心立方数(英語版)などが図付きで紹介されている。
グノモン編集
五角数とそのグノモン。色分けされた各部分がグノモンである。
先述のように、四角数からより大きな四角数を構成するときにはL字形の「部品」を付加すれば良かった。このような部品は古代ギリシアではグノモン(グノーモンとも、gnomon)と呼ばれた[10]。元々グノモンという語が意味するものは、日時計において影を作るための直立の棒であり、垂直を暗示するため、L字形の部品に対して用いられることとなった。エウクレイデス『原論』の第二巻では、正方形のみならず平行四辺形に対してグノモンという語をあてている。アレクサンドリアのヘロンは、その部品を付加することによって元の図形と相似な図形を得るようなもの、とした。矩形数の場合、L字形の部品を加えると、元の矩形と新しい矩形は縦横比が異なるため、厳密には相似とはいえないが、このような場合にもグノモンの語が用いられる。
13 + 23 + 33 + 43 = (1 + 2 + 3 + 4)2 を示す図。各グノモンの面積は立方数である。
西暦1000年頃、アラビア数学者アル=カラジ(英語版)は著書『ファフリー』(Fakhri)において、グノモンの考えを用いて三乗和の公式
を示した[11]。実際には彼は n = 10 の場合のみを説明しているが、疑いなく一般の場合を意識していた。四角数を用いた証明は以下の通り。ひとつの点から始め、一辺が 3 (= 1 + 2) の正方形となるようにグノモンを付加する。次は一辺が 6 (= 1 + 2 + 3) となるようにグノモンを付加する。これを繰り返して一辺が 55 (= 1 + 2 + … + 10) となるようにグノモンを付加したとき、最後のグノモンが含む点の個数は
10 × (1 + 2 + … + 9) × 2 + 10 × 10 = 103
と計算される。他のグノモンが含む点の個数も同様に立方数であることが分かるので、
13 + 23 + … + 103 = (1 + 2 + … + 10)2
が示される。
脚注編集
^ 例えば、MathWorld では figurate number を最も広い意味で用いている。
^ タッタソール著、小松尚夫訳『初等整数論9章』p. 12
^ 平方数である奇数までの和を考えることで、二辺の差が 1 であるピタゴラス数を得る。例えば、(1 + 3 + 5 + 7) + 9 = 52 より、42 + 32 = 52 といった具合である。ヒース pp. 37-38
^ a b ヒース p. 418
^ その著作は残っていないが、ディオファントスは、ヒュプシクレスを多角数を定義した人としてその定義を引用している。ヒース p. 311
^ ヒース p. 54
^ タッタソール p. 10
^ タッタソール p. 12
^ タッタソール pp. 15-20
^ ヒース p.36
^ ヒース pp. 55-56、カッツ p. 290
参考文献編集
T. L. ヒース著、平田寛、菊池俊彦訳、大沼正則訳『復刻版ギリシア数学史』共立出版、1998年(初版は1959年、原著は1931年出版)ISBN 978-4320015883
ヴィクター・カッツ著、上野健爾他訳『数学の歴史』共立出版、2005年 ISBN 978-4320017658
J. J. タッタソール著、小松尚夫訳『初等整数論9章』森北出版、2008年 ISBN 978-4627081628 - 特に、1.1節「多角数」
J. H. コンウェイ、R. K. ガイ著、根上生也訳『数の本』シュプリンガー・フェアラーク東京、2001年 ISBN 978-4431707707 - 特に、第2章「図を見てわかる数のしくみ」
関連項目編集
ウィキメディア・コモンズには、図形数に関連するカテゴリがあります。
http://ja.m.wikipedia.org/wiki/図形数
このコメントは投稿者によって削除されました。
素数を4で割って余りが1になるものは必ず二つの平方根の和で表せる。
teru2002さん 2013/10/19 00:04:38
素数を4で割って余りが1になるものは必ず二つの平方根の和で表せる。例えば、13は3×3+2×2、29は5×5+2×2、5は2×2+1×1・・・・・・
これを証明できる方いたらお願いします。
補足
おっとお、これを逆にすると限定的ではあるが素数が導き出せるぞ!不思議?それから奇数×奇数と偶数×偶数の組み合わせのパターンから素数になるみたいだぞ!驚きだ。2乗=平面だよね、つまり二つの平面の組み合わせから素数が生まれるのか・・・となると・・・二つの奇数×奇数×奇数と偶数×偶数×偶数の立体の組み合わせが残る素数に関係してるのでは・・・ということで後は皆さんも考えてください。
回答数:1 閲覧数:170 お礼:知恵コイン100
違反報告
ベストアンサー
nbr32nknshさん 2013/10/19 08:17:31
[teru2002SI]
「平方根」ではなく,「平方数」ですね.
4k+1型の素数が,2つの正の整数(奇数と偶数)の和にただ一通りに表されることは,フェルマーの二平方定理として古くから知られています.証明はオイラーによって与えられました.一般の整数が何通りの平方数の和(負数を含む順列の数)で表されるかはヤコービの二平方定理として知られています.証明はm^2+n^2=(m+in)(m-in)のように複素整数(ガウス整数)を使えば因数分解ができるので,因数分解の定理をガウス整数に拡張することによってなされます.Wikipediaの「二個の平方数の和」参照.
なお,補足はナンセンスです.二個の平方数の和が素数になるかどうかは判定のしようがありません.
違反報告
2ちゃんねる ★スマホ版★ ■掲示板に戻る■ 全部 1- 最新50
【訃報】伝説の数学者アレキサンダー・グロタンディークさん死去。86歳。フィールズ賞受賞者。__©2ch.net
1 :依頼@白夜φ ★@転載は禁止 ©2ch.net:2014/11/14(金) 18:09:41.06 ID:???
代表的数学者死去
20世紀で最も偉大な数学者の一人とされるアレキサンダー・グロタンディーク氏は、今週の木曜日にサン=ジロンの病院で亡くなりました。
ドイツ系フランス在住のアレキサンダー・グロタンディーク氏は1966年にフィールズ賞(数学のノーベル賞)を受賞し。
1990年代初め、彼は世界とのすべての接触を断ち村で隠遁生活に入りました。
彼の孤独な人生の終わりには、政治的エコロジーに深く関与し、彼は86歳で亡くなりました。
(翻訳:白夜φ ★)
▽元記事
LE FIGARO.fr
Deces d'une figure des mathematiques
http://www.lefigaro.fr/flash-actu/2014/11/14/97001-20141114FILWWW00035-deces-d-une-figure-des-mathematiques.php
▽関連記事
http://www.liberation.fr/sciences/2014/11/13/alexandre-grothendieck-ou-la-mort-d-un-genie-qui-voulait-se-faire-oublier_1142614
▽関連スレッド
グロタンディーク 追悼スレ [転載禁止](c)2ch.net
http://wc2014.2ch.net/test/read.cgi/math/1415948070/
アレクサンドル・グロタンディーク神
http://wc2014.2ch.net/test/read.cgi/math/1304116000/
2 :名無しのひみつ@転載は禁止:2014/11/14(金) 18:18:29.26 ID:rPy416iD
ご冥福をお祈り致します。
グロタンディークの著作をまとめてあるページへのリンクを貼っておきます。
どなたか「夢の鍵」を翻訳していただけないでしょうか・・・?
EGAやSGA,FGAなどの数学的著作はここからダウンロードできます。
http://webusers.imj-prg.fr/~leila.schneps/grothendieckcircle/pubtexts.php
「収穫と蒔いた種と」(Récoltes et Semailles)や
「夢の鍵」(La Clef des Songes)はここからダウンロードできます。
http://webusers.imj-prg.fr/~leila.schneps/grothendieckcircle/recoltesetc.php
「園の探求」(Pursuing Stacks)や「Galois理論を貫く長征」、
「デリヴァトゥール」、「プログラムの概要」、「子供のデッサン」、
セールやテイトなどとの書簡などはここからダウンロードできます。
http://matematicas.unex.es/~navarro/res/
3 :名無しのひみつ@転載は禁止:2014/11/14(金) 18:29:50.93 ID:xeq+0Gzo
南無。安らかに。
4 :名無しのひみつ@転載は禁止 ©2ch.net:2014/11/14(金) 18:35:57.71 ID:6jhMpXUR
>>1
「伝説の」ってアホか。普通に「大数学者」で良いだろ。
5 :名無しのひみつ@転載は禁止:2014/11/14(金) 18:37:03.63 ID:5+cW7hGW
>>4
伝説の、なんて言葉でもでも勘定が合わないくらいの、巨大な数学者だよ
6 :名無しのひみつ@転載は禁止:2014/11/14(金) 18:38:53.26 ID:jc31LGek
我が家では グロたん って呼んでいた
7 :名無しのひみつ@転載は禁止:2014/11/14(金) 18:42:50.98 ID:0Rt0SkTY
うちじゃダーグロだったなあ
8 :名無しのひみつ@転載は禁止:2014/11/14(金) 18:43:02.49 ID:M0nYf4J1
実物と影 美しいね
9 :名無しのひみつ@転載は禁止:2014/11/14(金) 18:43:53.15 ID:qR1T+aY9
だれ?
10 :名無しのひみつ@転載は禁止:2014/11/14(金) 18:44:09.03 ID:muK2/9rD
>>5
エクストリーム数学?
11 :名無しのひみつ@転載は禁止:2014/11/14(金) 18:49:52.53 ID:5+cW7hGW
>>9
グロタンディークの紹介に対して「フィールズ賞受賞者」なんて
紹介の仕方をしたら、グロタンディークをひどく矮小化してしまうレベルの
巨人
>>10
高度に抽象的かつ構造的かつ強力な「現代数学」像は
この人によって創始された。
12 :名刺は切らしておりまして@転載は禁止:2014/11/14(金) 18:52:41.43 ID:M0nYf4J1
気が付いたのはガロアなんだけどな
13 :名無しのひみつ@転載は禁止:2014/11/14(金) 19:02:35.38 ID:rWPhXwME
隠遁生活とかペレリマンかよ。
14 :名無しのひみつ@転載は禁止:2014/11/14(金) 19:05:38.15 ID:TaTO0Gt5
山奥でよく生存確認できたな
15 :名無しのひみつ@転載は禁止:2014/11/14(金) 19:07:01.24 ID:HiXXZ8hu
マイナー数学専門誌に論文を投稿して、その専門誌が世界中の数学者に知られるようになったこともある。
16 :名無しのひみつ@転載は禁止:2014/11/14(金) 19:12:21.89 ID:Z80p1OkP
>彼の孤独な人生の終わりには、政治的エコロジーに深く関与し、
エタールコホモロジーから政治的エコロジーへ
エタールコホモロジー - (タール + ホモ) = エコロジー
やっぱ煩悩が必要だな 数学者にも
17 :名無しのひみつ@転載は禁止:2014/11/14(金) 19:21:56.47 ID:b5UmRq7y
訃報(とほう)です。 <元ミス慶応 よ・し・え
18 :名無しのひみつ@転載は禁止:2014/11/14(金) 19:42:49.76 ID:YjXnIsW3
隠遁生活が伝説を作ったんだろうな
19 :名無しのひみつ@転載は禁止:2014/11/14(金) 20:01:20.25 ID:TaTO0Gt5
長生きしたな
20 :ココ電球_/ o-ν ◆tIS/.aX84. @転載は禁止:2014/11/14(金) 20:16:42.63 ID:qazgIlKs
やはりこの人も畳の上では死ねなかったな
21 :ココ電球_/ o-ν ◆tIS/.aX84. @転載は禁止:2014/11/14(金) 20:18:46.46 ID:qazgIlKs
潮改2の装備 なんだこれはー
22 :名無しのひみつ@転載は禁止:2014/11/14(金) 20:33:14.25 ID:djDq1Hz1
左翼に騙されなければ
こんな悲惨な最期にならずに済んだろうに
23 :名無しのひみつ@転載は禁止:2014/11/14(金) 20:48:22.93 ID:/tCtay9E
しかし数学者って、隠遁とかいろいろ変わり者が多いような気がする
24 :名無しのひみつ@転載は禁止:2014/11/14(金) 21:20:45.55 ID:9OoSJ/dD
神が死んだのか
25 :記憶喪失した男@転載は禁止:2014/11/14(金) 21:29:48.93 ID:27dKgKyt
おお。
著作は無料で公開されてるのか。
さすがだな。
26 :記憶喪失した男@転載は禁止:2014/11/14(金) 21:39:56.01 ID:27dKgKyt
ABC予想の望月教授の理論の土台を作った数学者
としか知らないけど。
27 :名無しのひみつ@転載は禁止:2014/11/14(金) 22:08:18.25 ID:Z1TWYe+T
私の父ちゃんはそれ程有名な学者ではなかったですが私にとってヒーローでした。
父ちゃんとグロタン氏にご冥福を
28 :名無しのひみつ@転載は禁止:2014/11/14(金) 22:31:00.16 ID:Cb3TtB0H
逸話[編集]
自然数57は「グロタンディーク素数」と呼ばれる。
もちろん57は素数ではないが、これは、グロタンディークが素数に関する一般論について講演をした際に、
具体的な素数を用いて例を挙げることを求められたとき、彼が誤って57を選んだことに由来する。
http://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%AC%E3%82%AF%E3%82%B5%E3%
83%B3%E3%83%89%E3%83%AB%E3%83%BB%E3%82%B0%E3%83%AD%E3%82%
BF%E3%83%B3%E3%83%87%E3%82%A3%E3%83%BC%E3%82%AF
http://d.hatena.ne.jp/junhigh/20040718
以前から気になっていたが、調べるでもなく放置していることがあるものだ。そのようなものは、時として、意識化されながら、明滅しながら放置されていく。
気になっていたことの一つに、「ガウスの逸話」がある。小学生の低学年の頃、先生からから「1から100まで足しなさい」と出題され、わずかの時間で答えたというものである。
どうして、気になっていたのかは、これは実話なのかというものである。たまたま読んでいた「現代思想」7月号の飯田隆の論にこの話が出ていて、ネットでちょっと調べてみた。
ウィキペディアによると
http://ja.wikipedia.org/wiki/%E3%82%AB%E3%83%BC%E3%83%AB%E3%83%BB%E3%83%
95%E3%83%AA%E3%83%BC%E3%83%89%E3%83%AA%E3%83%83%E3%83%92%E3%83%
BB%E3%82%AC%E3%82%A6%E3%82%B9
子供の頃から彼は神童ぶりを発揮し、逸話として、小学校での話がのこっている(彼は後年好んでこの話をしたそうだ)。ある時、1から100までの数字すべてを足すように課題を出された。それを彼は、1+100=101、99+2=101、98+3=101・・・となるので答えは101*50=5050だ、と即座に解答して教師を驚かせた。実際、算術の教師は彼の才能を見るにつけ、このような天才に自分が教えられることは何もないと言ったそうである。
どうも、ほんとうらしい。
別のサイトでは
http://www.geocities.co.jp/Technopolis/9874/episode1.html#gaus
数学、天文学、物理学とあらゆる分野で活躍した天才。幼少より神童ぶりを発揮した。小学校3年生の時に「1から100までの数を全て足すと、いくつか」という問題に対して、彼は瞬時に答えを出した。驚いた先生が解き方を質問すると「1と100を足すと101、2と99を足しても101.だから101を50個足すと5050」と明快に答えた。その先生は、もうガウス少年には教えることがないと悟り、高校生の使う数学書をとり寄せて与えた。
かなり、逸話は発展している。
さらに、次のサイトの説明が、僕が聞いた逸話に一番近い。
http://research.nii.ac.jp/~uno/algo_1.htm
高名な数学者(ガロアだったか、ガウスだったと思うんですが、なにせ、小学校のときに見た本の記憶なもので)の、小学校時代の逸話を紹介しましょう。彼が小学生だったとき、ある算数の授業で、彼の先生は、ちょっと楽をしようと思い、生徒たちにこんな課題を出したそうです。
「1から100までの数を全て足した数を計算しなさい」
これを計算するには99回足し算をする必要がありますから、しばらくは休めるなと思ったわけです。しかし、先生がやれやれ、と自分の席につこうとすると、生徒の一人だった彼は、たちどころに、「できました」と答えたそうです。そんなばかな、と先生がチェックしに行くと、確かに5050という正解が書いてあります。別に彼はそろばんの段位を持っていたわけではなく、計算が超人的に速かったわけではないのに、どうしてこんなことができたのでしょうか? その秘密は、彼の計算方法にあります。彼はこう考えました。
「1 と 100 を足すと 101、2 と 99を足すと 101、3 と 98 を足すと 101。このように、数を2つずつの組にすると、それぞれの合計が 101 になるように組み分けできる。組の数は全部で50。101 が 50 個あるのだから、全部あわせれば 5050だ。」
このように、この逸話の出所はわからないが、多くのサイトでこの話がとりあげられている。一般的には、1からnまでの和はn(n+1)/2で与えられる。飯田隆もこの証明をとりあげていたが、普通は、数学的帰納法でおこなうものである。別の証明が面白かった。
1+ 2 + 3 +・・・・・+n
n+nー1+nー2+・・・・・+1
対応する上下の項を足すと、すべて(n+1)で、それがn個ある。
この2行の和はn(n+1)であり、1行分の和は半分だから、
n(n+1)/2 となる。
/\
/\ / \
/ \ / \
/ \ / \
/ \/ /\ \
\ /\ \/ /
\ / \ /
\ / \ /
\/ \ /
\/
素数を4で割って余りが1になるものは必ず二つの平方数の和で表せる。
4k+1型の素数が,2つの正の整数(奇数と偶数)の和にただ一通りに表されることは,フェルマーの二平方定理として古くから知られています.証明はオイラーによって与えられました.一般の整数が何通りの平方数の和(負数を含む順列の数)で表されるかはヤコービの二平方定理として知られています.証明はm^2+n^2=(m+in)(m-in)のように複素整数(ガウス整数)を使えば因数分解ができるので,因数分解の定理をガウス整数に拡張することによってなされます.Wikipediaの「二個の平方数の和」参照.
http://ja.wikipedia.org/wiki/二個の平方数の和
この記事は「平方数」、「多角数定理」などの補遺に当たる。ここに示す事実は古くから知られている[1]ものであるが呼びかたが定まっておらず、フェルマーの4n+1定理[2]、フェルマーの二平方定理、あるいは単にフェルマーの定理(フェルマーの最終定理とは異なる)などと呼ばれる。
4を法として1に合同な素数は二個の平方数の和で表される。合成数が高々二個の平方数の和で表されるための必要十分条件は、4を法として3に合同な素因数が全て平方(冪指数が偶数)になっていることである。この定理は、フェルマーによって提起され、オイラーによって解決された。
http://ja.wikipedia.org/wiki/平方剰余の相互法則
http://yojiseki.exblog.jp/10648806/
定本『隠喩としての建築』より
編集 | 削除
以下、定本『隠喩としての建築』より。
たとえば、ここにオレンジ、すいか、テニスボール、フットボールがある。
それらを記憶にとどめるためには分類するほかない。
A __________
/ \
/ \
| (果物) |
______|___ ___|______
/ |オレ \ / | \
/ \ ンジ\ /すいか/ \
| \___|__|___/ |
| (小) ___|__|___ (大) |
| /テニス| |フット\ |
\ /ボール/ \ボール\ /
\______|___/ \___|______/
| (ボール) |
| |
\ /
\__________/
ある人は、それらをオレンジとすいか(果物)、テニスボールとフットボール(ボール)に分けるだろうし、
他の人は、それらを形態によって、オレンジとテニスボール(小)、すいかとフットボール(大)に分ける
だろう。
いずれの分類もそれだけではツリーになる(図BおよびC)。
B ◯ C ◯
/\ /\
/ \ / \
/ \ 小さな球◯ ◯大きな卵形
/ \ / \ / \
果物◯ ◯ボール / \/ \
/ \ / \ / /\ \
/ \ / \ / / \ \
◯ ◯ ◯ ◯ ◯ ◯ ◯ ◯
オレンジ すいか テニス フット オレンジ すいか テニス フット
ボール ボール ボール ボール
二つを合わせると、セミ・ラティスになる(図D)。
D __◯__
__/ /\ \__
_/ / \ \_
果物◯ 小◯ ◯大 ◯ボール
|\ / \ / \ /|
| \/ \/ \/ |
| /\ /\ /\ |
|/ \ / \ / \|
◯ ◯ ◯ ◯
オレンジ すいか テニス フット
ボール ボール
それらを集合論的に示すと、図Aのようになる。しかし、後者は視覚化するのが難しいので、
一般に、われわれが明瞭に視覚化できるのは、ツリーであり、実際、自然都市のようにその
内部で集合がオーヴァーラップするようなセミ・ラティス構造を思いうかべねばならないと
き、それをツリーに還元してしまう傾向がある。
(略)
もしツリーが厳格に守られると、都市も組織も荒廃せざるをえない。現代都市計画はその
ようなものだとアレグザンダーはいう。ブラジリアのような人口都市における生活の荒廃感
はよく知られている。『いかなる有機体においても、過度の区画化と内的要素の解離は、き
たるべき崩壊の最初のしるしである。解離は社会においては混乱であり、個人においては分
裂病とさしせまった自殺の徴候である』(Chiristopher Alexander "A city is not a tree"
「都市はツリーではない」1965)。
(定本『隠喩としての建築』53〜59頁より)
復刊ドットコムからのお知らせです。
『小平邦彦』『数学』『物理』『科学・技術』『学習参考書教育書受験書』
に関連するリクエストにご投票、商品をご購入いただきました皆さまに
ご案内です。
日本人として初めて1954年にフィールズ賞を受賞した小平邦彦先生。先生の
生誕100年を記念して、先生の主著である『複素多様体論』を新装版として
お届けします!
――――――――――――――――――――――――――――――――――
▼『複素多様体論』(最終得票数 44票)に寄せられた復刊リクエスト
コメントはこちら
http://www.fukkan.com/fk/VoteDetail?no=10556&tr=s
『複素多様体の基本事項がここまで詳しく記述されている書物は海外の
ものを含めてもない。また、発刊当時にはこれらの内容を必修のものとは
考えていなかった物理学者が、今は弦理論の発展から、必要欠くべからざる
ものになっている。』
『これからの研究に使いたいので、永く手元においておきたい。』
『日本が世界に誇る頭脳のうちの1人、小平先生の著書が絶版とは信じら
れません。全ての科学の基礎である数学の名著が手に入らないということは、
将来の日本の姿を悲観せざるを得ません。』
(以上、リクエストコメントより)
――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――
■『新装版 複素多様体論』(最終得票数 44 票)
http://www.fukkan.com/fk/CartSearchDetail?i_no=68323576&tr=s
――――――――――――――――――――――――――――――――――
【著者】小平邦彦
【発行】岩波書店
【定価】5,616円(税込み)
【発送時期】2015/02/下旬
複素多様体に関して変形理論の発展を軸に解説した教科書。
複素多様体の入門から始めて、無限小変形、存在定理、完備性の定理、安定性
の定理などについて、予備知識を仮定せずていねいに解説する。
なお、本書の変形理論は、多様体上の楕円型線型偏微分作用素の理論に
基づく。藤原大輔氏による、その基本的な解説を付録として収めた。
▼目次
正則関数
複素多様体
微分形式、ベクトル束、層
無限小変形
存在定理
完備性の定理
安定性の定理
附録 多様体上の楕円型偏微分作用素(藤原大輔)
▼著者紹介
小平邦彦(こだいら くにひこ)
1915年-97年、東京生まれ。1938年東京大学理学部数学科卒。1941年同大学
物理学科卒。ジョンズ・ホプキンス大学、スタンフォード大学、東京大学、
学習院大学などで教える。1954年日本人で初めてフィールズ賞受賞。
専門は、代数幾何学、複素多様体論。著書に、『軽装版 解析入門Ⅰ、Ⅱ』
『複素解析』『幾何のおもしろさ』『幾何への誘い』『怠け数学者の記』
『ボクは算数しか出来なかった』(いずれも岩波書店刊)などがある。
――――――――――――――――――――――――――――――――――
■キーワード『小平邦彦』商品ページ
http://www.fukkan.com/list/isearch/?tagid=6716&tr=s
■キーワード『数学』商品ページ
http://www.fukkan.com/list/isearch/?tagid=691&tr=s
■キーワード『物理』商品ページ
http://www.fukkan.com/list/isearch/?tagid=805&tr=s
■キーワード『科学・技術』商品ページ
http://www.fukkan.com/list/isearch/?tagid=4386&tr=s
■キーワード『学習参考書教育書受験書』商品ページ
http://www.fukkan.com/list/isearch/?tagid=836&tr=s
――――――――――――――――――――――
なぜ分数の割り算は逆数をかけるのか? | パパが教える算数教室
http://manabi.matiralab.com/sansu-reciprocal/
なぜ分数の割り算は逆数をかけるのか?
- Tagged: 基礎
スポンサードリンク Ads by google
続き
この計算方法をよく使いますよね。
しかし、どうして分数の割り算をするときには逆数をかければよいのでしょうか?
割り算は分数であることを思い出す
つまり、割り算の結果は、分数になります。そして、この分数が通分できるのであれば、通分しなければなりません。
通分した結果、分母が1であれば分子が答え、すなわち商になります。
では、 はどのように、分数にできるでしょうか?
が分子で、 が分母となる、分数ができます。
すごい、見難いですね…。 子どものノートには、真ん中の線が長くなるように、書いてくださいね。
(追記 : この投稿の最後に、画像で見やすい式を追加しました!!)
そして、分数の分母が1であれば分子が答えになるので、この分数を、分母が1になるように計算しましょう。
分母の を1にするには、逆数である をかければ良いですね。
逆数の掛け算が現れる!
なんと!! 割り算の式から、掛け算の式に変化しました。
つまり、この式の変形の結果が、分数の割り算は、逆数をかければ良い。という事がわかります。
いかがでしたか? 小学校の時に習ったから、なんとなーく逆数をかければ良い。と思っていた papa & mama さんも、お子さんに質問されたら説明してあげてくださいね♪
数学のトリビアを扱った本は多いが、こうした基礎をわかりやすく説明した本は少ない。
著者は経済学者だが、教育からやり直さなければと考えたのだろう。
再刊を望む。
『算数から数学へ』moreinfo
目次:
はしがき
第I部 代数の考え方――方程式を解く
第1章 方程式を使って鶴亀算を解く
1 鶴亀算を解く
2 方程式を使って鶴亀算を解く
3 分数と循環小数
第2章 連立二元一次方程式を解く
1 連立二元一次方程式をグラフで解く
2 負数を考える
3 連立二元一次方程式の意味
第3章 二次方程式を解く
1 エジプトの問題
2 二次方程式を解く
3 因数分解
4 二次方程式の解を求める
5 バビロニアの問題
第4章 文明の誕生
第 II 部 幾何の考え方――図形を解く
第5章 三角形
1 三角形を考える
2 三角形の性質
3 三角形の中心
4 三角形の重心
第6章 円
第7章 最大最小問題
1 最短距離と直線
2 面積を考える
第8章 ピタゴラスの定理
第9章 相似と比例
第10章 軌跡
第11章 作図
第12章 ギリシアの数学
追記:
宇沢弘文は2014年に亡くなられ、数々の追悼特集雑誌が出た。現代思想201503で柄谷行人が書いた文章はkindleサンプルで読める。
柄谷は社会的共通資本(財)という宇沢のアイデアを賞賛しているが、『算数から数学へ』第四章のエッセイ「文明の誕生」などは柄谷の世界史構想と重なるのではないか?
http://daily.2ch.net/test/read.cgi/newsplus/1426644828/-100
【話題】あなたは解けるかな? 小学4年生の図形の問題が超難問だと話題に [トゥギャッチ] [転載禁止]©2ch.net
1 :極限紳士 ★:2015/03/18(水) 11:13:48.00 ID:???*
難しすぎて大人でもなかなか解けない、小学4年生向けの問題が話題になっている。
https://pbs.twimg.com/media/CAOEW-sUUAAUvJP.png
Takuya @STYLE_S_Takuya
娘の算数の宿題が思わず難しかった。 これ、小4の問題か? 勿論、みんなは解けるよね?( ´,_ゝ`)
2015年3月16日 21:45
1センチ間隔で並んでいる点が頂点になる正方形を作る、算数の問題。2平方センチと5平方センチの二つの正方形を作らなければならない。長方形でいいなら、簡単な問題なのだが…。
正方形を半分にした三角形を利用すれば、解くことができるよう。
(答えなので注意)
https://pbs.twimg.com/media/CAQdOOdVAAAepRC.png
Takuya @STYLE_S_Takuya
解けてる人も多数いますが、回答を。 残念ながら娘は解けなかったので分からないという事で提出し、考え方は理解しろと言いました。
色んな解き方が有るとは思いますが私なりの考えはこうです。 平方根は使いません
2015年3月17日 08:53
縦や横にまっすぐ線を引いてもダメで、正解するには斜めになった正方形を描く必要がある。いったん長方形を作って、バラバラにしてから正方形にすると分かりやすいようだ。
必要な知識は少ないものの頭を柔らかくしないと解けないためか、正解の図形に驚きの声が集まっている。みなさんは答えが分かっただろうか?
http://i.imgur.com/CQDIbG5.png
http://i.imgur.com/aamoijb.png
ソース
トゥギャッチ
http://news.livedoor.com/article/detail/9898635/
2 :名無しさん@1周年:2015/03/18(水) 11:15:56.20 ID:3mbRmZV90
√2, √5 をグリッド上につくればいいだけ
むしろ大人が圧倒的に有利
17 :名無しさん@1周年:2015/03/18(水) 11:26:29.65 ID:U36mcbyY0
○ ○ ● ○
● ○ ○ ○
○ ○ ○ ●
○ ● ○ ○ ( ´∀`)
これは幾何というより分数の問題として考えるべきだ
対角線が1/2をつくる
あらゆるパターンがありえる
つまり分数は離散数学なのだ
今の算数及び数学は連続寄り過ぎる
>>17
10cm2
○ ○ ○ ● ○
● ○ ○ ○ ○
○ ○ ○ ○ ○
○ ○ ○ ○ ●
○ ● ○ ○ ○ ( ´∀`)
算術 - Wikipedia
ja.wikipedia.org/wiki/算術
算術 (さんじゅつ、英: arithmetic) は、数の概念や数の演算を扱い、その性質や計算 規則、あるいは計算法などの論理的手続きを明らかにしようとする学問分野である。「 算術」という日本語としては、文明開化前後の「数学」(mathematics) いわゆる西洋数学 の ...
四則演算-算術演算-関連項目
四則演算(シソクエンザン)とは - コトバンク
kotobank.jp/word/四則演算-667661
デジタル大辞泉 - 四則演算の用語解説 - 四則を用いてする演算。四則算。加減乗除。
辞書別に見る:世界大百科事典 第2版
つまり
分数は幾何なのだ
分数は幾何だが
日本語の問題でもある
1 と1/2
ピザ1枚 と 一切れ/二個に分けたうちの
個を分母に使うべきだということ
あるいは
リンゴ一個と
一切れ/2切れに分けたうちの
やはり最初がいい
数助詞を3つ使い分ける必要がある
「神」の数え方を教えてください。 - Yahoo!知恵袋 - Yahoo! JAPAN
detail.chiebukuro.yahoo.co.jp>...>一般教養
「神」の数え方を教えてください。 神に当てる助数詞(数助詞)としては、「柱(はしら)」「神 (しん)」「体(たい)」「座(ざ)」「尊(そん)」があります。【 柱 (はしら...
質問日:2008年4月26日
回答数:1件
助数詞 - Wikipedia
ja.wikipedia.org/wiki/助数詞
蚕 - 一頭(とう); 鏡 - 一面(めん); 掛け軸 - 一幅(ふく)、双幅の場合には一対(つい); 駕 籠 - 一挺(ちょう); 傘 - 一本(ほん)、和傘は一張(はり); 株式 - 一株(かぶ); 兜 - 一刎( はね); 神 - 一柱(はしら); (特定の場所に祀られている)神 - 一座(ざ...
日本語の助数詞-数詞と読み-文法-一覧
ヘブライの知恵
素数が神であり、なおかつ神の逆数であるモナドなのだ。
後者はドゥルーズの定義でライプニッツ自身は神を例外としていたが。
改訂版 経済学で出る数学: 高校数学からきちんと攻める | 尾山大輔, 安田洋祐
http://www.amazon.co.jp/dp/4535556598/
改訂前は秋山仁のインタビューが乗っていたが改訂版でカットされた
秋山氏と言えば以下の指摘が面白い。
読んで愉しい記事 【快文書館】(仮) 靴がそろえられれば数学は出来るか
http://bladerunner.tou3.com/Entry/659/
数学者の秋山仁は、中学高校までの数学だったか、とにかく数学ができるためには次の四つの能力があれば十分だ、とどこかで書い
ていた。
1 下駄箱に靴をそろえて入れることができる
2 辞書が引ける
3 カレーライスが作れる
4 最寄駅から自宅までの地図が描ける
1の靴をそろえられるということは「1対1の対応」の概念が理解できているということで、2の辞書が引ける、すなわち辞書で目的
の単語を見つけられるというのは「順序」の概念が分かっているということであり、3のカレーが作れるというのは「手順を整理し観
察・実行」ができるということを意味し、4の地図が描けるということは「抽象能力」がある(3次元のものを2次元に移して考え
られる、よけいな風景を省いて道順だけ抜き出して描ける、といった)……という意味だそうだ。
朝日社説?
一体一対応はフレーゲがヒュームの原理として展開しようとしたものだ。
改訂版 経済学で出る数学: 高校数学からきちんと攻める | 尾山大輔, 安田洋祐
http://www.amazon.co.jp/dp/4535556598/
定評のある本で、改訂前は秋山仁のインタビューが載っていたが改訂版でカットされたようだ
秋山氏と言えば以下の指摘が面白い。
http://bladerunner.tou3.com/Entry/659/
数学者の秋山仁は、中学高校までの数学だったか、とにかく数学ができるためには次の四つの能力があれば十分だ、とどこかで書い
ていた。
1 下駄箱に靴をそろえて入れることができる
2 辞書が引ける
3 カレーライスが作れる
4 最寄駅から自宅までの地図が描ける
1の靴をそろえられるということは「1対1の対応」の概念が理解できているということで、2の辞書が引ける、すなわち辞書で目的
の単語を見つけられるというのは「順序」の概念が分かっているということであり、3のカレーが作れるというのは「手順を整理し観
察・実行」ができるということを意味し、4の地図が描けるということは「抽象能力」がある(3次元のものを2次元に移して考え
られる、よけいな風景を省いて道順だけ抜き出して描ける、といった)……という意味だそうだ。
ちなみに一対一対応はフレーゲがヒュームの原理として展開しようとしたものだ。
改訂版 経済学で出る数学: 高校数学からきちんと攻める | 尾山大輔, 安田洋祐
http://www.amazon.co.jp/dp/4535556598/
定評のある本で、オススメ
改訂前は秋山仁のインタビューが載っていたが改訂版でカットされたようだ
秋山氏と言えば以下の指摘が面白い。
http://bladerunner.tou3.com/Entry/659/
数学者の秋山仁は、中学高校までの数学だったか、とにかく数学ができるためには次の四つの能力があれば十分だ、とどこかで書い
ていた。
1 下駄箱に靴をそろえて入れることができる
2 辞書が引ける
3 カレーライスが作れる
4 最寄駅から自宅までの地図が描ける
1の靴をそろえられるということは「1対1の対応」の概念が理解できているということで、2の辞書が引ける、すなわち辞書で目的
の単語を見つけられるというのは「順序」の概念が分かっているということであり、3のカレーが作れるというのは「手順を整理し観
察・実行」ができるということを意味し、4の地図が描けるということは「抽象能力」がある(3次元のものを2次元に移して考え
られる、よけいな風景を省いて道順だけ抜き出して描ける、といった)……という意味だそうだ。
ちなみに一対一対応はフレーゲがヒュームの原理として展開しようとしたものだ。
四則演算
http://itdoc.hitachi.co.jp/manuals/3020/3020645740/W4570093.HTM
(1) 四則演算の種類と機能
SQLの値式中に四則演算を使用した検索ができます。四則演算の種類と機能を次の表に示します。
表2-13 四則演算の種類と機能
四則演算 意味 機能
+ (単項演算) 正符号 符号を反転しません。
(2項演算) 加算 第1演算項に第2演算項を加えます。
- (単項演算) 負符号 符号を反転します。
(2項演算) 減算 第1演算項から第2演算項を減らします。
* (2項演算) 乗算 第1演算項に第2演算項を掛けます。
/ (2項演算) 除算 第1演算項を第2演算項で割ります。
(2) 四則演算結果のデータ型
第1演算項データ型が,SMALLINT,INTEGER,DECIMAL,SMALLFLT,及びFLOATの場合の,四則演算(2項演算)の演算項のデータ型と演算結果のデータ型の関係を次の表に示します。
表2-14 四則演算(2項演算)の演算項のデータ型と演算結果のデータ型の関係
第1演算項データ型 第2演算項データ型
SMALLINT INTEGER DECIMAL SMALLFLT FLOAT
SMALLINT INTEGER INTEGER DECIMAL SMALLFLT FLOAT
INTEGER INTEGER INTEGER DECIMAL FLOAT FLOAT
DECIMAL DECIMAL DECIMAL DECIMAL FLOAT FLOAT
SMALLFLT SMALLFLT FLOAT FLOAT SMALLFLT FLOAT
FLOAT FLOAT FLOAT FLOAT FLOAT FLOAT
そこで気晴らしのため友人である《普通》にまた違った問題を出してみることにした。 「 アメリカ ... う~ん。扉を変えます、たぶんそっちのほうが2倍当たると思います」 ... IQ228の天才、マリリン・ボス・サバントは新聞のコラム「マリリンに聞く」で「モンティ・ ホール問題」について投書を受け、「ドアを変更すると景品は2倍の確率でもらえる」と 回答。 一万通 ...
モンティ・ホール問題 - Wikipedia
ja.wikipedia.org/wiki/モンティ・ホール問題
ビジュアルエディターがウィキペディア日本語版にも導入されました(詳細)。 モンティ・ ホール問題. 出典: フリー百科事典『ウィキペディア(Wikipedia)』 ... 1990年9月9日発行 、ニュース雑誌 Parade にて、マリリン...
概要-ゲームのルール-直感と理論の乖離-ハズレに色を付ける方法
モンティ・ホール問題 IQ228のマリリン・ボス・サバント女史 自分のIQ ...
4knn.tv/iq-check/
マリリン・ボス・サバント モンティ・ホール問題 3つの扉の確率 3つの扉から正解を選ぶ 確率は1/3だ。 最初のドアをひとつ選ぶ。 そこから、主催者が、ハズレ一つを省く。 残り のドアは2つ。 確率は1/2になる…。はずだ。 だから最初に選んだドア ...
モンティホール問題のエクセレントな説明を見つけたんで紹介 - pal-9999 ...
d.hatena.ne.jp/pal-9999/20080326/p1
ベイズの定理と3囚人問題、モンティ・ホール問題を言葉だけで納得してもらう方法を 募集。 ... eggman 2009/10/20 12:59 マリリン・ボス・サバントもそういう説明をしたのに 、反論者たちには理解してもらえませんでしたね。 .... ってのが司会者からの本当の 問題と考えたほうが簡単ではないかと思います扉を変えることを選択する→最初の選択 は間違っていると答えると考えれば最初の選択は1/3の確率なので間違っ ...
マリリン・ボス・サヴァントが解いた問題ってど... - 数学 | Yahoo!知恵袋
detail.chiebukuro.yahoo.co.jp>...>数学
自分が解いてみたくて…ww無理なのはわかってます モンティホール問題wikiより参照 一種の心理トリックになっており、... ... 1990年9月9日発行、ニュース雑誌Paradeにて、 マリリン・ボス・サヴァントが連載するコラム欄「マリリンにおまかせ」において上記の読者 .... IQギネス保持者マリリンボスサバントさんに悩み相談をしたいのですが、英語で何と.
モンティ・ホール問題を解く - Qiita
qiita.com>Qiita>投稿>math
モンティ・ホール問題みなさんは有名なモンティ・ホール問題をご存知でしょうか。 ... ギネスブックで世界でも最も IQ が高いとされるマリリン・ボス・サバントは 1990 年、選び なおしたほうが選びなおさないより自動車が当たる確率は 2 倍になると ...
世界一IQが高い女性の悩み相談が秀逸な件。マリリン・ボス・サバント テッペン! 林先生の痛快!生きざま大辞典
http://youtu.be/tnBwaWVKjNA
ホールが無限にあってハズレを最後の一個まで消してくれたのと同じ
直感的な解釈
積分の定義方法の違いを直感的に理解できるように、山の(海抜より上の部分の)体積を計算する例
を考えよう。この山の境界ははっきりと定まっているとする(これが積分範囲である)。
リーマン積分による方法
ケーキを切るときのように、山を縦方向に切り分けて細分する。このとき、各パーツの底面は長方形に
なるようにする。次に、各パーツで最も標高が高いところを調べ、底面の面積とその標高を掛け合わせ
る。各パーツごとに計算したその値を足したものを、上リーマン和と呼ぶことにする。同様のことを、
最も標高が低いところに対して行い、下リーマン和と呼ぶことにする。分割を細かくしていったときに、
上・下のリーマン和が同じ値に収束するときに、リーマン積分可能であるといい、その極限値が山の
体積になる。
||
||||
||||||
||||||||
ルベーグ積分による方法
山の等高線を地図にする。等高線にそって地図を裁断して、地図をいくつかのパーツに分解する。
各パーツは面積を計算できる平面図形なので(測度が分かっているので)、パーツの面積とそのパーツ
の最も低い点の標高を掛け合わせる。各パーツのこの値を足したものを「ルベーグ和」と呼ぶことに
する。この「ルベーグ和」はルベーグ積分の構成にあった、単関数の積分に相当する。等高線の間隔
を半分にしていったときの「ルベーグ和」の極限値が山の体積になる。
__
____
______
________
ルベーグ積分30講
ルベーグ積分30講
A5/256ページ/1990年09月20日
ISBN978-4-254-11484-3 C3341
定価3,888円(本体3,600円+税)
志賀浩二 著
教科・科目 : 数学
#18より
日常的な例で,関数列fnがfにー様収束しないような状況を感じとってもらおう。
図31は,xy-平面上に底面がおかれた,1辺が1の立方体で,上面には大きさの違う
細かい穴が隙間のないほどいっぱいあいている.この上から細かい砂をー様に落とし
ていくとする,あるいは立方体の上面に箱を乗せ,そこに砂を詰めたと思ってもよ
い.砂は穴から下の立方体ヘと落ちていくが,穴の大きいところでは,砂はどんどん
高くなり,穴の小さいところでは,砂はごく微少な量だけ積もってくる.砂はあまり
崩れないとすると,この状況は図31で察せられるだろう.数学的に考えるときに
は,穴の大きさは(そしてまた砂粒の大きさも)いくらでも小さくとってもよいとす
る.このとき,立方体の底面(x , y)から測ったn秒後における,砂の高さをfn(x,y)
とすると,n→∞のとき,fn(x,y)→1である.これは,どの点(x,y)をとっても,
点(x,y)上で砂はいつかは立方体の上面にまで達するということである,しかし,
たとえば点(a,b)で上面の穴が小さければ,砂はごくわずかずつしか落ちないから
1万秒たっても,まだそこでの砂の高さは,1/1000に達していないかもしれない,
そのことは
f10000(a, b) < 1000
を示す,すなわち,非常に速く砂の高さが1に達する場所と,恐ろしいほど長時間た
ってから高さが1に達する場所とが散在している.このようなとき,fn(x , y)は1に
一様に収束していない.
n秒後の砂の体積を測ってみても,これが究極的には立方体を埋めつくし,体積1
となることは予想できないだろう.
単関数列が可測関数に収束する状況と積分の収束とがどのように関わるかにつ
いて,次講の最初で述べることにしよう,
________________
/|・・・・・・・・・・・・・・・/|
/・|・・・・・・・・・・・・・・/・|
/・・|・・・・・・・・・・・・・/・・|
/___|___________ /・・・|
|・・・・|・⇩・・・・・・・・・|・⇩・・|
|・・・・|・・・・・・・・・・・|・・・・|
|・・・・|・・・・・・⇩・・・・|・・・・|
|・・・⇩|・・・・・・・・・・・|・・・・|
|・・・・|___________|____|
|・・・/|(・・)・・・・・・・|(・)/|
|・・/・|・・・・・(・・)・・|・・/ |
|・/(・)・・・・・・・・・・・|・/ |
|/___|___________|/・ |
| | ・ | |
| | ・ ・ | ・ |
| ・| ・ | |
| | ・ | |
1| ・| ・ | |
| | | ・ |
| |_/\___/\___|____|y
| / / \ / \ |/\ /
| /・ \__// \ |--/
| / /\ \____/ | / 1
|/__--___________|/
x 1
2進数から10進数への変換
http://www.infonet.co.jp/ueyama/ip/binary/bin2dec.html
「423円」 と書けば、 百円硬貨 4 枚、 10 円硬貨 2 枚と 1 円硬貨 3 枚の、 「四百二十三円」 のことです。 10 進数の各桁には、それぞれ 102、101、100の重みがあるからです (この 10 を 「基数」 といいます)。
10進数の 423
2 進数 は 0 と 1 の、 2 つの数字だけで数値を表します。
10 進数の各桁に 10 倍の重みがあるように、 2 進数の各桁にもそれぞれ 2 倍の重みがあります。 2 進数の基数は 2 です。
2進数の 1101
したがって、 2進数の 1101 は、 1 × 8 + 1 × 4 + 0 × 2 + 1 × 1 = 13 (10進数) となります。
2 進数を 10 進数に変換するには、 このような計算をすればよいわけです。
下には、 8 桁の 2 進数が表示されています。 "STEP" ボタンをクリックすると、 10 進数に変換する過程が表示されます。
数値はキーボードで入力して変えることができますから、 いろいろ試してみてください。
数値は 2 進数 (BINary) でも、 10 進数 (DECimal) でも、 16 進数 (HEXadecimal) でも入力できます。
iPodから送信
メルセンヌ数
メルセンヌ数(メルセンヌすう、英: Mersenne number)とは、2の冪よりも 1 小さい自然数、すなわち 2n − 1(n は自然数)の形の自然数のことである。これを Mn で表すことが多い。2進数表記では、n 桁の 11…11 となる。
1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095, 8191, 16383, 32767, 65535, …(オンライン整数列大辞典の数列 A000225)
上記の数列において、素数であるメルセンヌ数をメルセンヌ素数(メルセンヌそすう、英: Mersenne prime)という。Mn が素数ならば n は素数であるが、逆に n が素数であっても Mn は素数とは限らない (M11 = 23 × 89)。後述するように、効率的な素数判定法によって、巨大な素数の実例としてメルセンヌ素数を発見することが特に興味の対象となっている。このため近年では、分散コンピューティングによるプロジェクト GIMPS (Great Internet Mersenne Prime Search) によるメルセンヌ素数の発見が進められている。具体的なメルセンヌ素数は
3, 7, 31, 127, 8191, 131071, 524287, 2147483647, …(オンライン整数列大辞典の数列 A000668)
である。詳しくは#発見されているメルセンヌ素数の表を参照のこと。
なお、「メルセンヌ数」という語で、n が素数であるもののみを指したり[1]、さらに狭くメルセンヌ素数を指す場合もある[2]。
目次
1 歴史
2 数学的性質
2.1 素因数
2.2 完全数
2.3 メルセンヌ素数
3 素数判定法
3.1 リュカ・テスト
3.2 リュカ-レーマー・テスト
4 発見されているメルセンヌ素数の表
5 未解決問題
6 脚注
7 参考文献
8 関連項目
9 外部リンク
歴史
1644年にマラン・メルセンヌは、2n − 1 が素数になるのは、n ≤ 257 では n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257 だけであると主張した。しかしその主張の一部は誤っていた。リストに含まれていない M61, M89, M107 が素数であり、リストに含まれている M67, M257 は合成数である[3][4]。
M31 は1772年、 レオンハルト・オイラー によって素数であると証明された[3][5]。
M127 は1876年、 エドゥアール・リュカ によって素数であると証明された[3][6]。
M61 が素数であることは、1883年にイヴァン・パヴシン(英語版)によって示された[3]。
M67 が素数でないことは、1903年10月、フランク・ネルソン・コールにより示された。彼はニューヨークで開かれたアメリカ数学会で 193707721 × 761838257287 を黒板に計算し、M67 と一致することを証明した。この間一言もしゃべらず、席に戻った後、少し間を置いて拍手が沸き起こったと伝えられている[7]。
1952年、ラファエル・M・ロビンソン が SWAC を利用して M521 から M2281 まで、5つのメルセンヌ素数を発見[3]して以降、発見にはコンピュータが使用されており、コンピュータの進歩と共に新たなメルセンヌ素数が発見されつつある。
数学的性質
Mn が素数ならば n は素数であるが、n が素数であっても Mn は素数とは限らない。前者の対偶である命題「n が合成数ならば Mn は合成数である」は次の式から示される[3][8]。
2ab − 1 = (2a − 1){1 + 2a + 22a + … + 2(b−1)a}
素因数
p が素数の時、Mp の素因数は 2p を法として 1 と合同[9]、かつ 8 を法として 1 または −1 と合同である[10]。また、p が 4 を法として 3 と合同なとき、Mp が 2p + 1 で割れることと、2p + 1 が素数であることは同値である[10]。また、Mp の最大の素因数 q は q ≥ c5 p log p(c5 は計算可能な定数)を満足する(Erdős-Shoreyの定理1)[11]。
完全数
Mp = 2p − 1 が素数であるならば、2p−1(2p − 1) は完全数となる[3][12]。この定理はすでに紀元前4世紀のエウクレイデス(ユークリッド)によって証明されていた[13]。およそ二千年の後に、全ての偶数の完全数はこの形の時に限るということが18世紀のレオンハルト・オイラーにより証明された。
完全数
Mp = 2p − 1 が素数であるならば、2p−1(2p − 1) は完全数となる[3][12]。この定理はすでに紀元前4世紀のエウクレイデス(ユークリッド)によって証明されていた[13]。およそ二千年の後に、全ての偶数の完全数はこの形の時に限るということが18世紀のレオンハルト・オイラーにより証明された[12]。
メルセンヌ素数
2016年10月現在、メルセンヌ素数は49個まで知られている。ただし、メルセンヌ素数としての番号が確定しているものは、45番目までであり、
p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667(オンライン整数列大辞典の数列 A000043, オンライン整数列大辞典の数列 A000668)における Mp がそうである。さらに46, 47, 48, 49番目の候補として p = 42643801, 43112609, 57885161, 74207281 が挙がっており、現在、間に素数がないかどうか検証中である。
分散コンピューティングによるプロジェクト GIMPS はメルセンヌ素数を発見することを目的としており、近年発見されたものは全てこのプロジェクトによるものである。
2004年5月15日、GIMPS は41番目の素数候補が発見されたことを発表した。検証後723万5733桁の数、224036583 − 1 が素数であることが確認された。
2005年2月27日、GIMPS は42番目の素数候補がドイツの眼科医によって発見されたことを報告した。781万6230桁の数、225964951 − 1 であり、[1]に掲載されている。
2005年12月15日、GIMPS は43番目の素数候補が米国のセントラル・ミズーリ州立大学(現セントラル・ミズーリ大学(英語版))の教授2名によって発見されたと報じた。230402457 − 1、915万2052桁 [2]。
2006年9月4日、GIMPS は44番目の素数候補が、43番目の素数候補を発見したのと同じ教授2名によって発見されたと報じた。232582657 − 1、980万8358 桁[3]。
2008年8月23日、GIMPS は46番目の素数候補が、カリフォルニア大学ロサンゼルス校の数学部のコンピュータによって発見されたと報じた。243112609 − 1、1297万8189 桁(十進法で表記すると 243112609 − 1 ≒ 3.1647 × 1012978188)[4]。発見順では45番目だが、次に発見されたメルセンヌ素数と発見時期が近かったため、46番目の候補として45番目の候補と同時に発表された。この素数は電子フロンティア財団が賞金をかけた1000万桁以上の最初の素数となるため、GIMPS によって同校数学部に50,000ドル、慈善事業に25,000ドル、残りを前の6つのメルセンヌ素数の発見者へ分配することになった。
2008年9月6日、GIMPS は45番目の素数候補が、ドイツで発見されたと報じた。237156667 − 1、1118万5272 桁[5]。これは、GIMPS によって発見された中では、発見順序と桁数が逆転した初めてのケースである。
2014年11月8日、232582657 − 1 が公式に44番目のメルセンヌ素数であると報じた[6]。
素数判定法
メルセンヌ数が素数かどうかを調べるための判定法としてリュカ・テスト (Lucas test) とリュカ-レーマー・テスト (Lucas-Lehmer primality test) がある。
リュカ・テスト
p が (4j + 3) 型の素数のとき、S0 = 3, Sn = Sn−12 − 2 (n ≥ 1) と定義すると、
ならば、Mp は合成数である。
ならば、Mp は素数である[14][15][16]。
証明については「リュカ・テストの証明」を参照
リュカ-レーマー・テスト
デリック・ヘンリー・レーマー(英語版)は、エドゥアール・リュカの判定法を改良し、今日ではリュカ-レーマー・テスト (Lucas-Lehmer primality test) と呼ばれる、メルセンヌ数に対する素数判定法を確立した。
p が奇素数のとき、Mp が素数となるための必要十分条件は、S0 = 4, Sn = Sn−12 − 2 (n ≥ 1) と定義したときに Sp−2 が Mp で割り切れることである[17][18][19]。
リュカ-レーマー・テストは二進計算機用のアルゴリズムに向いており、コンピュータによるメルセンヌ素数の発見には、この判定法が用いられてきた。例えば、2p ≡ 1 (mod Mp) より、A・2p + B ≡ A + B (mod Mp) が成り立つので、Mp で割る割り算の代わりに、二進法で p 桁のシフト演算と足し算だけで計算できる。
現在「最大の」素数がメルセンヌ素数である理由はこの判定法にあると言える。
証明については「リュカ-レーマー・テストの証明」を参照
発見されているメルセンヌ素数の表
オンライン整数列大辞典の数列 A000668
# p Mp Mp の
桁数 発見日 発見者
1 2 3 1 紀元前5世紀[20] 古代ギリシアの数学者
2 3 7 1 紀元前5世紀[20] 古代ギリシアの数学者
3 5 31 2 紀元前3世紀[20] 古代ギリシアの数学者
4 7 127 3 紀元前3世紀[20] 古代ギリシアの数学者
5 13 8191 4 1456年 不明[21]
6 17 131071 6 1588年 ピエトロ・カタルディ(英語版)
7 19 524287 6 1588年 ピエトロ・カタルディ
8 31 2147483647 10 1772年 レオンハルト・オイラー
多様体 - Wikipedia
多様体 - Wikipedia
https://ja.wikipedia.org/wiki/多様体
多様体(たようたい、英: manifold, 独: Mannigfaltigkeit)とは、局所的にはユークリッド空間と見なせるような図形や空間(位相空間)のことである。多様体上には好きなところに局所的に座標を描き込むことができる。
多様体の歴史はゲッティンゲンで行われたリーマンの講演に始まる。
多様体論は、ロバチェフスキーの双曲幾何学によって始まった非ユークリッド幾何学やガウスの曲面論を背景として様々な幾何学を統一し、 n 次元の幾何学へと飛躍させた。発見当初はカント哲学に打撃を与えたりした非ユークリッド幾何学も多様体論の一例でしかなくなってしまった。
リーマンがゲッティンゲン大学の私講師に就任するために行った講演『幾何学の基礎に関する仮説について』の中で「何重にも拡がったもの」と表現した概念が n 次元多様体のもとになり n 次元の幾何学に関する研究が始まった。この講演を聴いていたガウスがその着想に夢中になり、(ガウスは普段はあまり表立って他人を褒めることはなかったが、)リーマンの着想がいかに素晴らしいかを同僚に語り続けたり、帰り道にうわの空で道端の溝に落ちたりしたと言われている。
年表 編集
1826年『平行線公準の厳密な証明』(ロバチェフスキー)
1827年『曲面の研究』(ガウス)
1829年『幾何学の新原理並びに平行線の完全な理論』(ロバチェフスキー)
1854年6月10日『幾何学の基礎に関する仮説について』(リーマン)
1872年エルランゲン目録(クライン)
1895年『位置解析』(アンリ・ポアンカレ)
1916年一般相対性理論(アルベルト・アインシュタイン)
1936年『微分可能多様体』(ハスラー・ホイットニー(英語版))
ホーム
http://kok.on.coocan.jp/book/book0894.htm
2006.01.03 国家の品格 藤原正彦 新潮文庫 新潮新書141 数学者の藤原さんだが、いつになく、ストレートにずけずけと、 酒でも飲んでくだを巻くような調子で書いている。いつもは単刀直 入だが、もう少しひねった言い方をしていたはずだ。それだけ最近 の日本の状況について、歯がゆさというより危機感を抱いているの かもしれない。気取ったものいいでは一般には伝わらないというこ とか。
藤原が講師を勤めたNHKの教育でやっていた「天才の栄光と挫 折」という番組の中で、インドのラマヌジャンという数学者の話が でてくる。毎日のように、なぜ思いつくのか不思議に思えるような 美しい定理を発見するのだが、自分ではその証明ができない。藤原 はその才能の秘密を探ってインドまで足を運ぶ。ラマヌジャンの生 まれた町を訪れたときに、その疑問が解ける。藤原はそこで、バラ モン教寺院の建築の息を飲むような美しさに打たれたのだ。このよ うな美しい建築の中で生まれ育ったとすると、あの不可解だが美し い数学の定理の数々を思いつくのも納得できたという。バラモンと はインドの階級の中でもっとも上位に位置づけられる階級である。 物質的な現実の処理能力はないから経済的には恵まれないが、その 知識や精神性の高さによって尊敬をうける存在である。寺院建築に みられるような、ある種の「美」に対する感覚、これを担っている のがバラモンである。ラマヌジャンも家は極貧を極めたが、石版に 数式を書きつけて毎日を過ごすラマヌジャンを許すという環境があ った。藤原は、そうした「美しさ」に対する感覚、精神性の高さが 国家には必要だと語る。
そのひとつの象徴が、藤原によると武士道だという。日本はかつ ては武士道という精神的な柱を持っていた。国家を引っ張るエリー トとして武士がいた。やはり物質的には恵まれない場合もあったが 漢文などの学識、身体の鍛練など高貴な精神性を担っていた。武士 は食わねど高楊枝である。藤原は父親、新田次郎の影響もあってか 英雄主義的な指向もある。明治期のエリートの伝統を引き継いでい る面もあるのだろう。そうした日本が本来持つ優れた「国柄」が、 最近の国際化の中で失われつつあるという。 まず、近代的合理精神の限界を指摘する。先進国においても社会 の荒廃が進行している。それは近代的合理精神にたよりすぎている からだという。 近代的合理精神が拠り所とする「論理」だが、論理を徹底すれば 問題が解決できるという考え方は誤りである。全てについて論理を 徹底することはできないし、人間にとって重要な価値について論理 は教えてくれない。論理は前提を必要とするが、前提が正しいかど うかはわからない。モデル化した前提に論理を組み立てても適用範 囲はおのずと限られたものでしかない。論理は何段階か経ると急速 に複雑さを増し、正しいかどうか判断するのが難しくなる。コンピ ュータでさえ計算不可能な論理はいくらでもあるのだ。 こうした論理の上にたつ西欧の自由、平等、民主主義も実は疑わ しい。自由と平等の概念はフィクションである。民主主義の前提条 件である「成熟した国民」など存在しない(このへんはプラトンの ようなエリート主義である)。また自由と平等は、両立しえない。 その点、日本は論理とは異なる「形」と「情緒」によって国が支 えられている。自然への感受性、もののあわれ、懐かしさ、惻隠の 情といったもの。いきづまりの西欧に比べて、日本のこうした美徳 のほうが可能性がある。仏教、禅における無常観やもののあわれと いったものが日本人の精神的な土壌となっている。それを象徴する のが茶道、花道、書道、そして武士道である。藤原は武士道のテキ ストとして新渡戸稲造「武士道」をあげる。 なぜ「情緒と形」が大切なのか。 ①日本だけにとどまらない普遍的価値。跋扈するグローバリズムは アメリカの戦略にすぎず画一化を進めるものである。能率、効率と いった価値に対抗するものとして「情緒と形」の意味は大きい。 その他、②文化、学問の基礎 ③国際人にとって必要 ④人間本来 の総合判断力 ⑤人間中心主義の抑制 ⑥戦争をなくすための手段 といった点があげられる。 最後に国の力とはなにか。結局は人間の力である。そして人間の 力を引き出すには品格ある国家たることが必要である。品格ある国 家は天才を育てる。それが冒頭のラマヌジャンの例である。日本は 戦前まで保っていた品格を戦後のアメリカ化の中で失いつつ有る。 数学などはすでにアメリカのレベルになってしまったという。 最後に品格のある国家の指標として4点あげている。 ①独立不羈 ②高い道徳 ③美しい田園 ④天才の輩出 少々気負い過ぎている部分もあるが傾聴すべき話でもある。21 世紀の日本の国家の形を考える上でのひとつのテキストではある。 内容的には、養老などが言っていることと重なる部分も多い。すで に明らかに方向性は見えてきているのだ。その状況証拠のひとつと なる本だ。
138『心は孤独な数学者』 藤原正彦 初版1997年: さくらの読書スイッチ
http://book-sakura.cocolog-nifty.com/blog/2009/11/1381997-eaa9.html
◆ラマヌジャンの公式を見て感じる感嘆と苛立ち
ラマヌジャンは、「我々の百倍も頭がよい」という天才ではない。「なぜそんな公式を思い付いたのか見当がつかない」という天才なのである。アインシュタインの特殊相対性理論は、アインシュタインがいなくとも、2年以内に誰かが発見しただろうと言われる。数学や自然科学における発見のほとんどすべては、ある種の論理的必然、歴史的必然がある。だから「10年か20年もすれば誰かが発見する」のである。
ラマヌジャンの公式を見て私が感ずるのは、まず文句なしの感嘆であり、しばらくしてからの苛立ちである。なぜそのような真理に想到したかが理解できないと、その真理自体を理解した少なくとも私はなれないのである。
数学では、大抵の場合、少し考えれば必然性も分る。ところがラマヌジャンの公式群に限ると、その大半において必然性が見えない。ということはとりもなおさず、ラマヌジャンがいなかったら、それらは100年近くたった今日でも発見されていない、ということである。
◆ラマヌジャンの独創の源泉
マドラスに戻った私は、再びラマヌジャン高等数学研究所にランガチャリ教授を訪れた。彼にどうしても聞きたいことが私にはあった。ラマヌジャンの独創の源泉に関するランガチャリ教授の見解である。ラマヌジャンとは同一宗派、同一カースト、同一職業の人だから、何か興味があることが聞けるかも知れない、と考えたのである。
普段なら打てば響くように応答する彼が、しばらく間をおいてから、「チャンティング(詠唱)が独創の一因と思う」、と言った。詠唱とは詩文などに単調なメロディーをつけて唱えることである。ヒンドゥー寺院を訪れると、小声で歌うように祈禱文を詠唱している人をよく見かけるが、独創との関係が私にはよく分からない。
狐につつまれた思いで彼の顔を覗き込むと、「インドでは古代より、数学と文学は混淆していました」、と言う。ランガチャリ教授は、独創との関連をなお把握できないでいる私には構わず続ける。「インドでは長い間、教科書でさえすべて詩文で書かれていたのです」、「国語と数学の教科書がですか」、「違います。理科も社会もです。子供たちはそれを詠唱により頭に入れたのです。独創との関連について述べてみましょう。まず、詠唱により大量の知識を大量に蓄えることができます。次に一つ一つの知識が孤立した点でなく、広がりを持って記憶されるということです」。
これで得られるのはいくつかの基礎知識ばかりではない。孤立点としての知識は結ばれ、広がっており、大規模な鳥瞰さえ与えている。ガンジス河口で糸をたれる釣り人は、ヒマラヤの氷河に思いを馳せることさえできるのである。一見無関係なもの同士を結ぶ糸を発見するのが独創なら、鳥瞰図つきの知識はきわめて有用のはずである。
ランガチャリ教授はさらに、「折にふれ口ずさむことは、得られた知識や概念をもてあそぶということです」。数学上のひらめきは、頭の中やノート上で対象をもてあそんでいるうちに得られることが多い。孤立した知識に比べ、連想的に結びついた知識は、引き出してもてあそびやすいうえ、詠唱することはそのままもてあそぶことになるとも言えよう。私はランガチャリ教授が、言葉少なながら、心理学上の本質的な問題を提起しているように感じた。
clover著者
Hujiwaramasahiko_2藤原 正彦(ふじわら まさひこ、1943年7月9日 - )は、満州国新京生まれの数学者、エッセイスト。専門は数論、特に不定方程式論。
戦後いずれも作家となった新田次郎、藤原てい夫妻の次男として、満州国の新京に生まれる。ソ連軍の満州国侵攻に伴い汽車で新京を脱出したが、朝鮮北部で汽車が停車したため、日本への帰還の残る区間は母と子3人による1年以上のソ連軍からの苦難の逃避行となった。母親の機転がなければ死亡、よくて残留孤児になっていたであろう。
アメリカ留学記『若き数学者のアメリカ』(1977年)が話題となり、日本エッセイスト・クラブ賞を受賞。以後エッセイストとして人気を博している。身辺雑記からイギリス滞在記や科学エッセイ、数学者の評伝に至るまで対象は広く、端正な文章とユーモア溢れる筆致にファンが多い。
エッセイではしばしば「武士道」や「祖国愛(ナショナリズムではなくパトリオティズム)」、「情緒」の大切さを諧謔を交えて説いてきたが、そのエッ センスを平易な語り口でまとめた『国家の品格』(2005年11月、新潮新書)が200万部を超えるベストセラーとなり、翌2006年の新語・流行語大賞 に選ばれるなど大きな話題となった。同書では数学者の立場でありながら、あえて「論理より情緒」「英語より国語」「民主主義より武士道」と説いている。
橋本麻里さんがリツイート
1時間
職業的ディレッタント @hide36ous
2017は素数やから単体ではおもろいネタがないとか言うてる人おるけど、任意の4k+1型の素数は二平方の和で書ける(Fermatの定理)し、ちゃんとZ[i]上では素元分解できるんやからな!!!
2017=(44+9i)(44–9i)
あけましておめでとうございます。
━━━━━━━━━━━━━━┓
┃
┃
┃
┃
┃
┃
┃
┃
┃
┃
┃
┃
┃
┃
━━━━━━━━━━━━━━┛
┏━━━━━━━━━┓
┃ ┃
┃ ┃ ┃
┃ ┃ ┃
┃ ┃ ┃
┗━━━━┛ ┏━━━━┛
┃
┃
┃
┃
┏━━━━┓ ┗━━━━┓
┃ ┃ ┃
┃ ┃ ┃
┃ ┃ ┃
┃ ┃
┗━━━━━━━━━┛
┓ ┏━━━┓ ┏━━━┓
┃ ┃ ┃ ┃ ┃
┏━┛ ┗━┓ ┗━┛ ┏━┛
┃ ┃ ┃
┃ ┏━┓ ┃ ┏━┓ ┗━┓
┃ ┃ ┃ ┃ ┃ ┃ ┃
┗━┛ ┗━┛ ┃ ┗━━━┛
┃
┏━┓ ┏━┓ ┃ ┏━━━┓
┃ ┃ ┃ ┃ ┃ ┃ ┃
┃ ┗━┛ ┃ ┗━┛ ┏━┛
┃ ┃ ┃
┗━┓ ┏━┛ ┏━┓ ┗━┓
┃ ┃ ┃ ┃ ┃
━┛ ┗━━━┛ ┗━━━┛
┏━┓┏━┓┏━┓┏━┓┏━┓
┗┛┏┛┗┓┗┛┏┛┗┓┗┛┏┛
┏┓┗┓┏┛┏┓┃┏┓┃┏┓┗┓
┃┗━┛┗━┛┃┗┛┗┛┃┗━┛
┗┓┏━━┓┏┛┏┓┏┓┃┏━┓
┏┛┗┓┏┛┗┓┃┗┛┃┗┛┏┛
┃┏┓┃┃┏┓┃┗┓┏┛┏┓┗┓
┗┛┗┛┗┛┗┛┏┛┗━┛┗━┛
┏┓┏┓┏┓┏┓┗┓┏━┓┏━┓
┃┗┛┃┃┗┛┃┏┛┗┓┗┛┏┛
┗┓┏┛┗┓┏┛┃┏┓┃┏┓┗┓
┏┛┗━━┛┗┓┗┛┗┛┃┗━┛
┃┏━┓┏━┓┃┏┓┏┓┃┏━┓
┗┛┏┛┗┓┗┛┃┗┛┃┗┛┏┛
┏┓┗┓┏┛┏┓┗┓┏┛┏┓┗┓
┗━┛┗━┛┗━┛┗━┛┗━┛
┏━━━━┓
┃ ┃ ┃
┗━┛ ┏━┛
┃
┏━┓ ┗━┓
┃ ┃ ┃
┗━━━━┛
┏━━━━━━━━━┓
┃ ┃
┃ ┃ ┃
┃ ┃ ┃
┃ ┃ ┃
┗━━━━┛ ┏━━━━┛
┃
┃
┃
┃
┏━━━━┓ ┗━━━━┓
┃ ┃ ┃
┃ ┃ ┃
┃ ┃ ┃
┃ ┃
┗━━━━━━━━━┛
┓ ┏━━━┓ ┏━━━┓
┃ ┃ ┃ ┃ ┃
┏━┛ ┗━┓ ┗━┛ ┏━┛
┃ ┃ ┃
┃ ┏━┓ ┃ ┏━┓ ┗━┓
┃ ┃ ┃ ┃ ┃ ┃ ┃
┗━┛ ┗━┛ ┃ ┗━━━┛
┃
┏━┓ ┏━┓ ┃ ┏━━━┓
┃ ┃ ┃ ┃ ┃ ┃ ┃
┃ ┗━┛ ┃ ┗━┛ ┏━┛
┃ ┃ ┃
┗━┓ ┏━┛ ┏━┓ ┗━┓
┃ ┃ ┃ ┃ ┃
━┛ ┗━━━┛ ┗━━━┛
┓┏━┓┏━┓
┏┛┗┓┗┛┏┛
┃┏┓┃┏┓┗┓
┗┛┗┛┃┗━┛
┏┓┏┓┃┏━┓
┃┗┛┃┗┛┏┛
┗┓┏┛┏┓┗┓
┛┗━┛┗━┛
┓ ┏━━━┓ ┏━━━┓
┃ ┃ ┃ ┃ ┃
┏━┛ ┗━┓ ┗━┛ ┏━┛
┃ ┃ ┃
┃ ┏━┓ ┃ ┏━┓ ┗━┓
┃ ┃ ┃ ┃ ┃ ┃ ┃
┗━┛ ┗━┛ ┃ ┗━━━┛
┃
┏━┓ ┏━┓ ┃ ┏━━━┓
┃ ┃ ┃ ┃ ┃ ┃ ┃
┃ ┗━┛ ┃ ┗━┛ ┏━┛
┃ ┃ ┃
┗━┓ ┏━┛ ┏━┓ ┗━┓
┃ ┃ ┃ ┃ ┃
━┛ ┗━━━┛ ┗━━━┛
┃
┃ ┓
┏━━━━┓ ┗━━━━
┃ ┃ ┛
┃ ┃
┃ ┃ ┓
┃ ┃
┗━━━━━━━━━┛
1:55 午前
yoji said...
┏━┓┏━┓┏━┓┏━┓┏━┓
┗┛┏┛┗┓┗┛┏┛┗┓┗┛┏┛
┏┓┗┓┏┛┏┓┃┏┓┃┏┓┗┓
┃┗━┛┗━┛┃┗┛┗┛┃┗━┛
┗┓┏━━┓┏┛┏┓┏┓┃┏━┓
┏┛┗┓┏┛┗┓┃┗┛┃┗┛┏┛
┃┏┓┃┃┏┓┃┗┓┏┛┏┓┗┓
┗┛┗┛┗┛┗┛┏┛┗━┛┗━┛
┏┓┏┓┏┓┏┓┗┓┏━┓┏━┓
┃┗┛┃┃┗┛┃┏┛┗┓┗┛┏┛
┗┓┏┛┗┓┏┛┃┏┓┃┏┓┗┓
┏┛┗━━┛┗┓┗┛┗┛┃┗━┛
┃┏━┓┏━┓┃┏┓┏┓┃┏━┓
┗┛┏┛┗┓┗┛┃┗┛┃┗┛┏┛
┏┓┗┓┏┛┏┓┗┓┏┛┏┓┗┓
┗━┛┗━┛┗━┛┗━┛┗━┛
2:24 午前
yoji said...
上の図はペアノ(Peano)曲線と呼ばれるもので、下の図の左のように、最初の単純な曲線を半分に
縮小し、向きを変えて4枚貼り合わせます。
次に線で結びます。これを繰り返すとどんどん複雑になって無限に繰り返すと正方形を埋め尽くします。
自己相似形の繰り返しという意味でフラクタルになっています。
フラクタルの例 ペアノ曲線のつくり方
図の右側のように4枚張り合わせるときに少し隙間を空ける(半分ではなく隙間分考えて縮小しておく)
と下のようになりフラクタルらしいフラクタル図形になります。
【サッカー】くじ「BIG」で宇宙誕生レベルの奇跡が起こる 運営側「全くの偶然」その確率は0.0000000000000000000000000000001%以下 [無断転載禁止]©2ch.net
1 : Marine look ★@無断転載は禁止2017/02/20(月) 21:09:00.28 ID:CAP_USER9
25溝0316穣0000杼0000垓0000京0000兆0000億0000万0000分の1の奇跡
http://image.itmedia.co.jp/nl/articles/1702/20/l_ikko_BIG001.jpg
ランダムで試合結果を予想するスポーツくじ「BIG」で、14試合×5口分の予想結果が一致したという画像が投稿され物議を醸した件で、日本スポーツ振興センターが見解を発表しました。
システムの不具合や不正操作によるものではなく、全くの偶然によるものと結論づけられています。
その確率は約2,503,160,000,000,000,000,000,000,000,000,000分の1。単位を追加すると約25溝0316穣0000杼0000垓0000京0000兆0000億0000万0000分の1となります。
「BIG」は、1口分14試合に“ホームチームの90分勝ち”“ホームチームの90分負け”“その他”の3パターンの予想結果を3分の1ずつランダムに割り当て、実際の試合結果に応じて当せん金が当たるというサッカーくじ。
ネット掲示板で5口分が完全一致した画像が投稿されたことをきっかけに「不正操作ではないか」などの臆測を呼んでいました。
発表では「このくじの販売元である『楽天totoサイト』を運営する楽天に実際に販売されていたことを確認した」としていますが、「重複する投票内容の出現はあり得る」「システム不具合や不正な操作によるものではない」と偶然によるものとされています。
日本スポーツ振興センターに「現実的に起こり得ない確率で不正を疑う声もある。返金するなどの対応はしないのか」と問い合わせたところ、「返金の予定はない」と回答しました。
http://headlines.yahoo.co.jp/hl?a=20170220-00000060-it_nlab-sci
関連
【サッカー】toto・BIG運営が発表「不具合や不正な操作等によるものではない。」 5口分の投票内容が一致していた事例について★2 [無断転載禁止](c)2ch.net
http://hayabusa8.2ch.net/test/read.cgi/mnewsplus/1487591566/
2 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:09:14.45 ID:4pXt8cD40
1/300 ←パチンコで当たる確率
1/330,000 ←麻雀で天和を上がる確率
1/4,800,000 ←totoBIGの一等当選確率
1/6,000,000 ←LOTO6の一等当選確率
1/10,300,000 ←LOTO7の一等当選確率
1/100,000,000 ←1つの精子が受精する確率
1/77,000,000,000,000 ←他人とDNAが一致する確率
1/1,000,000,000,000,000,000,000,000 ←ビッグバンが起こったり、人が壁をすり抜ける確率
1/2,500,000,000,000,000,000,000,000,000,000,000 ←サッカーくじBIGで起こった確率
3 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:09:38.57 ID:IeTNOBwQ0
そうなんだ
4 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:10:09.04 ID:IF4Y+sYP0
宇宙ヤバイ
5 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:10:09.46 ID:VAnzPNAO0
つまりどういうことだってばよ
6 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:10:13.46 ID:Mcudbkgw0
これ楽天が客には絶対当たらない番号渡して、実際はクジを買わずに呑んでたんじゃないか
7 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:11:13.15 ID:XRd+3zNi0
画像が捏造なんじゃないの?
8 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:11:15.16 ID:yC/rY2Ji0
人が壁をすり抜ける確率よりも低いw
9 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:11:22.31 ID:wHPD80O+0
楽天が悪いの?
totoBIGのシステムが悪いの?
totoBIGのシステム自体が悪いなら
もうtotoBIG買えないやん
10 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:11:31.09 ID:Lz80/vfP0
まぁ当然嘘だけど認めるわけにはいかないよな
過去の販売実績全部返金しないといけなくなるもんな(笑)
11 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:11:51.99 ID:ZullE4w90
はじめに5口買っててその翌日に10口買うってのもなんか不自然だな
12 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:12:00.02 ID:vxAVIi/k0
これイカサマあるよって認めたようなもんじゃねーか
13 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:12:00.71 ID:OVRf4opU0
アブダクションだよスカリー
14 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:12:04.93 ID:b61bOx890
溝って単位があるのを初めて知った
15 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:12:06.24 ID:UCqyMuj70
>全くの偶然
この言い分は厳しいわ。誠実さにかけるわ。
「起こり得ないことがおきた」ことは認めないと。
16 : 名無しさん@恐縮です@無断転載は禁止2017/02/20(月) 21:12:13.07 ID:8mQ0Ng890
ある人が5週連続で1等をあてる確率
17 : @無断転載は禁止2017/02/20(月) 21:12:12.96
確率論分かってないアホが多すぎだろw
中学か高校で習うことだぞw
BIG(ランダムの3択抽選)で70回連続で前回と同じ数字がでる確率 1/(3^70)=1/(2.5*10^33)
どのくらいかというと
サイコロで1が連続43回出る確率 1/(6^43)=1/(2.8*10^33)
麻雀で天和(テンホウ)が6局連続でる確率 1/(330000^6)=1/(1.3*10^33)
このくらいなら、まれによくあるレベル
イカサマでもなんでもない
はい論破
| /
| /
| /
|___/
|__/3倍
|_/2倍
|/1倍
ーーーーーーーーX0倍ーーーーーーー
-1倍/|
/_|
/__|
/ |
/ |
/ |
/ |
マイナスの倍数をイメージすると0倍も単なる通過点とわかる
この場合
ゼロは数というより場所、位置にすぎない
848 : 名無しのひみつ@無断転載は禁止2017/04/14(金) 10:30:39.33 ID:XnNUzOi8
零に何回、零足しても零だからでしょ。
849 : 名無しのひみつ@無断転載は禁止2017/04/14(金) 17:35:33.59 ID:BzPLw/OH
5に0回5を足すと0?
850 : 名無しのひみつ@無断転載は禁止2017/04/14(金) 17:42:10.55 ID:AFHO9k/T
5×5=0+5+5+5+5+5
5×0=0(0に5を一度も足さない)
という式に表すと分かりやすいかも。
851 : 名無しのひみつ@無断転載は禁止2017/04/14(金) 17:44:46.01 ID:AFHO9k/T
でも乗法を累加法と同一視する解釈には限界がある。
面積で体感させるべきかもしれない
___
I I
I I
I___I 3×3
___
I___I1×3
_ 0×1
__ 0×3
______________ … 0×∞
2017/04/14(金) 20:11:00.20 ID:vicWEOeo
こういう表をつくって、じっと眺める。縦の列、横の列の法則性を考えながら
そうすると
掛け算にゼロがからむとゼロになることも
マイナスとマイナスの掛け算がプラスになることも
掛け算の順序を逆にしても値が変わらないことも
納得できるんじゃないのかな
https://walshmath01056.wikispaces.com/file/view/integer_multiplication_table_Nik_%26_Nicko.gif/237288441/integer_multiplication_table_Nik_%26_Nicko.gif
紐よりも
球の表面積が円の面積の4倍であることの証明
https://youtu.be/pNEsgJLCL8Q
階段にペンキを塗る量で検証したらいい
【インド】最古の「ゼロ」文字、3~4世紀のインド書物に 英大学が特定[09/16] [無断転載禁止]©2ch.net
1虎跳 ★2017/09/16(土) 11:10:11.16ID:CAP_USER
最古の「ゼロ」文字、3~4世紀のインド書物に 英大学が特定
【9月16日 AFP】3~4世紀のインドの書物に記された黒い点が、数字の「0(ゼロ)」の最古の使用例であることを、英オックスフォード大学(University of Oxford)のチームが特定した。
この書物は、1881年に現パキスタン国内に位置する村で発掘されたカバノキの樹皮の巻物で、発見場所の村の名前にちなみ「バクシャーリー(Bakhshali)写本」と呼ばれている。1902年からオックスフォード大学のボドリアン図書館(Bodleian Libraries)で保管されてきた。
バクシャーリー写本は、すでにインド最古の数学書であるとされていたものの、その年代についてはこれまでさまざまな意見が飛び交っていた。しかし同図書館の科学者チームが放射性炭素年代測定したところ、制作時期がこれまで考えられていたよりも約500年さかのぼる3~4世紀であることが判明した。
ゼロの最古の使用例はこれまで、インド・グワリオル(Gwalior)の寺院の壁に残る9世紀の碑銘だとされていた。ゼロを意味する文字はマヤやバビロニアといった古代文明でも使用されていたが、現在使われている「0」記号の起源は古代インドで使用されていた点記号だった。(c)AFP
AFP
http://www.afpbb.com/articles/-/3143151?cx_part=topstory&cx_position=3
http://afpbb.ismcdn.jp/mwimgs/a/a/700x460/img_aa9cfbc7b13f4704be444d27e347b918216862.jpg
【数学】〈続報〉「ABC予想(オステルレ・マッサー予想)」望月教授による証明が数学界を二分
30コメント17KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1しじみ ★2017/12/24(日) 06:13:10.02ID:CAP_USER>>3>>12
数学の難問「ABC予想(オステルレ・マッサー予想)」を証明したとする、
京都大学の望月新一教授による論文について、世界の数学者らは様々な形で受け止めている。
理解できる人が世界で20人ほどの500頁にわたる望月氏の著名な論文を、望月氏本人が率いる科学雑誌が掲載に向け受理したのだ。
査読雑誌に科学論文が掲載されるということは、関係分野の有能な専門家らがその論文を終わりまで読み評価したことを意味する。
つまり必要な水準の査読のもと、その過程で誤りや捏造の確率は最小限にまで低められるのだ。
京大の数理解析研究所が発行する数学誌面で、ABC予想を証明する望月氏の論文が2018年初めに掲載される見通しになっている。
この論文は既に2012年に完成していたもので、その長さは500頁にわたる。
この掲載については朝日新聞が報じている。ところが、この論文の掲載は望月氏の大勢の同僚にとって、
査読者らが同論文を最後まで読み承認したということを意味することにはならない。
ABC予想の証明に際しての問題は、論文の執筆者以外では誰もその証明を理解できないという点である。
掲載に向け論文を受理した雑誌の編集長が、望月氏自身であるという事実も疑念を呼んでいる。
「ABC予想」は1980年代に提示され、現代整数論の未解決問題として長い間残ったままだった。
この予想を証明するため、望月氏は新たな数学的手段「p 進数タイヒミューラー理論(p-adic Teichmüller theory)」を構築した。
ABC予想について、この理論に基づいて組み立てられた証明を評価するために、
英オックスフォードと京都で2回にわたって国際会議が開かれた。
現在、この証明について討論できる能力のある人の数は20人とみられている。
しかし、これら「身を捧げた人々」の中に、望月氏の論文をより広い範囲の研究者らに説明できる人が一人もいないことがわかったため、
学会は依然として懐疑的な態度を崩していない。
今回のニュースについてニュージーランド・カンタベリー大学の数学者、
フェリペ・ヴォロシュ氏は、「掲載に向け(論文が)受理されたという事実は、私にとっては何かを変えるものではない。
依然として私は、理解できる形での説明を待っている状態だ」とコメントしている。
一方、ヴォロシュ氏と違う意見を持っているのが、英ノッティンガム大学の数学者、イヴァン・フェセンコ氏だ。
フェセンコ氏は、望月氏による証明を完全に理解し、証明に誤りを発見していない数少ない研究者の一人だ。
フェセンコ氏は、論文は既に検証されており、日本の雑誌に掲載されるという事実は、
関係する分野をリードする専門家らが日本出身であるということで説明できると主張している。
この雑誌は論文そのものについて、画期的な業績であり、過去半世紀にわたる整数論の歴史の中で最高の成果であると評価している。
しかし、数学界の多数派がフェセンコ氏に同意するためには、望月氏による証明の内容を把握できるだけでなく、それを他の人に説明できる人が現れる必要がある。
望月氏は、ロシアの数学者であるグリゴリー・ペレルマン氏と比較される。
ペレルマン氏は、「ミレニアム問題」の一つ、「ポアンカレ予想」を証明したことで知られる。
2006年には「フィールズ賞」、10年には米クレイ数学研究所からミレニアム問題の一つを解決した業績に対し賞が授与されることが決まったが、
ペレルマン氏はこれらの受賞を辞退した。その後ペレルマン氏は研究活動を中止し、メディアによる取材を拒否している。
望月氏は1969年東京生まれ。16歳で米プリンストン大学数学科に入学し、1994年に日本に帰国した。
同僚らは、望月氏が数学の問題を解く際高い集中力を発揮すること、米国文化を嫌っていること、
日本を去る気がないことを指摘している。
関連スレ
【数学】数学の超難問・ABC予想を「証明」した望月教授の論文がPRIMSに掲載決定
https://egg.5ch.net/test/read.cgi/scienceplus/1513365315/
スプートニク
https://jp.sputniknews.com/science/201712214404570/
【数学】〈テキストファイルで22.6MB〉「史上最大の素数」約2年ぶりに更新、50番目のメルセンヌ素数で桁数は2324万9425桁
94コメント24KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1しじみ ★2018/01/05(金) 11:54:02.65ID:CAP_USER>>43
新たなメルセンヌ素数を探している「グレート・インターネット・メルセンヌ数検索(GIMPS)」が、
既知の素数として最大のものとなる50番目のメルセンヌ素数を見つけました。新たな素数は「2 77,232,917-1」で、
「M77232917」と呼ばれています。
50th Known Mersenne Prime Discovered
https://www.mersenne.org/primes/press/M77232917.html
関連画像
https://i.gzn.jp/img/2018/01/05/largest-known-prime-number/01.png
メルセンヌ素数とは、「2のべき乗より1小さい自然数」であるメルセンヌ数の中でも素数のものを指します。
GIMPSによると50番目のメルセンヌ素数「M77232917」は2324万9425桁の数字で、
これまで最長だった49番目のメルセンヌ素数「M74207281」の2233万8618桁と比べて、約100万桁大きくなっています。
以下のZIPファイルには、「M77232917」の書かれたテキストファイルが入っています。
ZIPファイルのサイズは11MBほどですが、テキストファイルは22.6MBあります。
http://www.mersenne.org/primes/digits/M77232917.zip
関連画像
https://i.gzn.jp/img/2018/01/05/largest-known-prime-number/02.png
「M77232917」は2017年12月26日に、
GIMPSにボランティアとして参加しているジョナサン・ペース氏のコンピューターが発見したとのこと。
ペース氏はテネシー州ジャーマンタウン在住の51歳の電気技師で、
これまで14年にわたってGIMPSプロジェクトに協力してきました。
今回の発見で、ペース氏にはGIMPS研究発見賞として3000ドル(約34万円)が贈られます。
なお、素数であることの証明は、Intel i5-6600プロセッサを搭載したPCなら、
6日間ノンストップで計算を続ける必要があります。
今回は、4つの異なるハードウェア構成の上でそれぞれ異なる4つのプログラムを使い、独立した検証が行われました。
GIMPSは新たな素数を見つけるために1996年にジョージ・ウルトマン氏が結成した組織で、
公式サイトで公開されているソフトを使い、誰でも素数探索に参加することができます。
1996年11月にジョエル・アンメルガード氏が35番目のメルセンヌ素数を見つけて以降、この50番目のメルセンヌ素数まで、
16個のメルセンヌ素数を続けて発見しています。
GIGAZINE
https://gigazine.net/news/20180105-largest-known-prime-number/
【歴史】〈画像あり〉行間には直筆のメモ (清の第4代皇帝)康熙帝が学んだ数学書『原論』満州文字版を公開
6コメント3KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1しじみ ★2018/01/10(水) 19:50:01.25ID:CAP_USER>>5
【1月8日 CNS】
古代ギリシャ数学を代表する数学書『原論』の満州文字版が、
中国・内モンゴル自治区(Inner Mongolia Autonomous Region)フフホト市(Hohhot)の
内モンゴル自治区図書館(Inner Mongolia Library)で公開されている。
満州文字版は、古代ギリシャの数学者ユークリッド(Euclid)の著書を、
清朝時代に中国で活動していたフランスのイエズス会士、ジョアシャン・ブーヴェ(Joachim Bouvet)と
張城(Zhang Cheng)が編集・翻訳した。この数学書は当時の清朝皇帝、
康熙帝(Kangxi Emperor)が幾何学を学ぶために作成された書で、
すべて手書きの満州文字で書かれている。
行間には、康熙帝が学習する際に記したと思われる赤い字で書かれた直筆のメモが残っており、
『国家珍貴古籍名録』に登録されている。
同図書館で開催中の『冊府千華——内モンゴル自治区蔵国家珍貴古籍特展』で、
宋、元、明、清時代の150件の古代書籍と共に公開されている。
書籍は漢字のほか満州文字、モンゴル語、チベット語、西夏文字などさまざまな文字で記されている。
雷峰塔(Leifeng Pagoda)が倒壊した際に発見された北宋時代の仏教の教典『宝篋印(ほうきょういん)陀羅尼(だらに)経』など
貴重な古籍が公開されている。(c)CNS/JCM/AFPBB News
画像一覧:満州語版の『原論』。康熙帝の手書きのメモが残されている
http://afpbb.ismcdn.jp/mwimgs/9/0/700x460/img_902b6a37a3692a1397e6ac83457cfb40237420.jpg
http://afpbb.ismcdn.jp/mwimgs/d/3/700x460/img_d358ad1aa95150fb759c7175ddfdb933230805.jpg
http://afpbb.ismcdn.jp/mwimgs/5/7/700x460/img_57b63f1d4574011cf1d638cd98ad2ab8255124.jpg
http://afpbb.ismcdn.jp/mwimgs/6/5/120x/img_65bf81404d95412f167a71da38801ce170016.jpg
AFP
http://www.afpbb.com/articles/-/3156941
学校では教えてくれない数学:勉強メモ - livedoor Blog
blog.livedoor.jp/calc/archives/7898322.html
これは、いわゆるバーンサイド予想(アーベル群でない有限単純群の位数は偶数である)を肯定的に解決・証明したもので、この功績により、トンプソンは1970年にニースで開かれた国際数学者会議で、フィールズ賞を授与された。なお、この予想の証明は、200 ページ以上にわたる背理法を使ったもので、長い考察の結果、矛盾を出すものらしい。 ちなみに、フェイトは、この証明で用いられている表現論の箇所をサポートしたらしい。 ( 4)置換群 置換群のうち、代表的な対称群を、互換を生成元とみなして ...
確率と割合とは、それぞれつぎのようになります。
確率は、できごとが起こる確かさの程度を示したもの
割合は、全体にたいして一部が占める比率
見出し [非表示]
1 確率
2 割合
3 できごとが起こる・起こらないの話のときは確率
確率
できごとがどのくらい起こりやすいか考えるときには、確率と呼びます。ものごとが起こる確かさの程度は、全体にたいして、その対象のできごとが起こる割合であらわすのです。
割合をつかっているわけですが、ある現象、できごとが起こる・起こらないの話で割合をつかうときには、確率、となるのです。
割合
割合は、全体と一部があるものであれば、すべてに使うことができます。どのくらい占めているかを示したもので、現象の起こりやすさだけではありません。
日本のすべての家庭でペットを飼ってい家庭の割合
宝くじすべての枚数のなかに1等が入っている割合
このように「割合」をつかいますよね。
できごとが起こる・起こらないの話のときは確率
でも、目の前にあるこの1件の家に入ったら、その家でペットが飼われているか?を確認するのであれば、「この家でペットが飼われている確率は…」と言うことになります。
また、今から買う宝くじが当たるのか?という話であれば、「宝くじが当たる確率は…」となります。
これらは、
家の中に入ったらペットがいるというできごと
宝くじを買って当たるというできごと
なので、確率となるのです。
https://toukeigaku-jouhou.info/2018/01/06/difference-of-probability-and-raito/
【数学】〈最小超置換問題〉「涼宮ハルヒの憂鬱」のおかげで25年解けなかった数学の難問が解決されるかもしれない[10/25]
47コメント36KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1しじみ ★2018/10/25(木) 13:26:58.20ID:CAP_USER>>20>>47
海外の掲示板「4chan」での議論が、数学者を25年以上悩ませてきた「The Minimal Superpermutation Problem(最小超置換問題)」という難問を解決するかもしれないと、世界中の数学者から大きな関心を集めています。解決の糸口となったのは、テレビアニメ「涼宮ハルヒの憂鬱」のエピソードの視聴順についてでした。
https://i.gzn.jp/img/2018/10/25/suzumiya-haruhi-superpermutation/00.jpg
サムネイル読み込み中···
/sci/ - The Haruhi problem (lower bound) - Science & Math - 4chan
http://boards.4chan.org/sci/thread/10089701/the-haruhi-problem-lower-bound
An anonymous 4chan post could help solve a 25-year-old math mystery - The Verge
https://www.theverge.com/2018/10/24/18019464/4chan-anon-anime-haruhi-math-mystery
2006年に放送されたテレビアニメ「涼宮ハルヒの憂鬱」の第1期は全14話から構成されています。2006年のテレビ放送時では、物語の時系列と異なる順序でエピソードが放映され、話題となりました。
4chanのアニメファンコミュニティの間では「涼宮ハルヒの憂鬱」をどのエピソード順に見るのがよいかという話題がしばしば取り扱われていました。その中で「可能な限りの順序で全てのエピソードを見たい場合、最も少ない組み合わせは何通りになるか」という問題が提起され、このテーマはやがて「Haruhi Problem(ハルヒ問題)」という問題に昇華し、数学コミュニティで議論されるようになりました。このハルヒ問題は、数学の世界では「最小超置換問題」と呼ばれる難問にあたります。
「最小超置換」とは、全ての組み合わせを内包した文字列のこと。例えば、A・Bという2要素の組合せは「AB」と「BA」となりますが、この2文字の最小超置換は「ABA」となります。「ABA」という最小超置換文字列には、「AB」と「BA」という2通りの組み合わせが内包されています。
https://i.gzn.jp/img/2018/10/25/suzumiya-haruhi-superpermutation/aba_m.jpg
サムネイル読み込み中···
また、A・B・Cという3要素の組み合わせは「ABC」「ACB」「BAC」「BCA」「CAB」「CBA」の6通り。そして3文字の最小超置換は「ABCABACBA」という9文字の文字列となります。「ABCABACBA」という文字列には、6通りの組み合わせが全て内包されています。
https://i.gzn.jp/img/2018/10/25/suzumiya-haruhi-superpermutation/abcabacba_m.jpg
サムネイル読み込み中···
この最小超置換の文字列の長さは、要素が増えるごとに爆発的に増えると考えられています。記事作成時点では、最小超置換の文字数は4要素までしか判明していません。最小超置換問題とは、要素の数を「n」と置いたときに最小超置換の文字列の定式化とその証明を求めるというものでした。
この問題が論文で提起されたのは1993年のことでしたが、25年以上かけてこの問題が解決されることはありませんでした。しかし、4chanの数学フォーラムで、nを14とするハルヒ問題の解法をきっかけに証明が投稿され、論文という形式ではないものの、最小超置換問題の解決の糸口となるのではと世界中の数学者から注目を集めました。
https://i.gzn.jp/img/2018/10/25/suzumiya-haruhi-superpermutation/snap0733_m.png
サムネイル読み込み中···
マケット大学の数学者であるジェイ・パントーン氏は、当初この投稿の内容に懐疑的でしたが、この投稿を元にした論文(PDFファイル)を発表しています。パントーン氏によると、「涼宮ハルヒの憂鬱」のエピソードを全組合せで視聴するには少なくとも939億2423万411話のエピソードを見る必要があるとのこと。
また、コンピュータ科学者のロビン・ヒューストン氏は以前から最小超置換問題に取り組んでいた数学者で、ハルヒ問題を皮切りに数学の難問が解き明かされようとしていることについて「興味深い状況だ」と興奮しています。
■論文
https://docs.google.com/viewer?a=v&pid=forums&srcid=MTUwMTUxMjExNDk4NTk5NjY5OTkBMDMxNDgwMTA5ODA5OTYyNzcyNDQBdlNFMnM3eTVCUUFKATAuMQEBdjI&authuser=0
http://mathsci.wikia.com/wiki/The_Haruhi_Problem
GIGAZINE
https://gigazine.net/news/20181025-suzumiya-haruhi-superpermutation/
知恵蔵の解説
多様体
局所座標系を関数で貼り合わせてできる図形を、多様体という。例えば、提灯を作る時、竹などでできた枠に紙を貼って作る。紙の上に座標系を書いておけば、2枚の紙が重なる点は提灯の上では同じ点になり、2枚の紙の上の2点が貼り合わされる。この時、紙の上の座標系が局所座標系であり、できた提灯が多様体である。数学では、この貼り合わせを関数で行う。貼り合わせの関数が、連続関数の時は位相多様体、無限回微分可能の時は微分可能多様体、正則関数の時は複素多様体と呼ぶ。またいくつかのn変数多項式の共通零点を多項式関数で貼り合わせてできる多様体を、代数多様体という。19世紀中頃、リーマン(G.F.B.Riemann)がリーマン面を概念化したのが多様体の始まり。
(桂利行 東京大学大学院教授 / 2007年)
出典 (株)朝日新聞出版発行「知恵蔵」知恵蔵について 情報
66ニュースソース検討中@自治議論スレ2019/03/12(火) 16:32:07.35ID:HfXXGtkF>>70
>>49
サインは、半径1の同心円上のある点のy座標の値
コサインは、同じくx座標
タンジェントは、x/y
ここまでパラメータは中心角ど
ログは指数関数の逆関数
67ニュースソース検討中@自治議論スレ2019/03/12(火) 16:33:28.84ID:5xJTIzC9>>68
>>58
あと、理科の科学専門用語とか、基本的に明治知識人の漢文教養ベースに翻訳造語されているんで、
漢文の読み下し文ルールなんかと組み合わせて教えると、断然理解しやすくなる。
現行教育って知識が教科別に分断されているせいで、本来は体系化して身に着けられるべき知識が
断片化して丸暗記を強いている側面が凄くあると思うわ。
68ニュースソース検討中@自治議論スレ2019/03/12(火) 16:37:20.38ID:HfXXGtkF
>>67
はー、なるほどね
もう英語の読んじゃうな、めんどくせーから
69ニュースソース検討中@自治議論スレ2019/03/12(火) 16:38:24.77ID:yTlHEXY/>>71>>73>>77
中学生教えてると一番困るのが三角関数なんだよな~
俺はもうそういうもんだって刷り込んでるから
生徒にこの利点何って言われても説明がだるい
70ニュースソース検討中@自治議論スレ2019/03/12(火) 16:38:48.70ID:5xJTIzC9>>75
>>66
tangentが英語の原義は「接線」だと教えれば、さらに理解が早くなる。
教科ごとの「術語」を教えるのには漢文教育と同時に英語教育も効くのだ。
関数の≪…数学ダンス…≫の姉妹編は、自然数の数の言葉ヒフミヨ(1234)のダンスに絵本「もろはのつるぎ」を観る。
円周率と素数に隠された不思議な関係… 【ゆっくり解説】
https://youtu.be/qs6-nISCYtg
円周を最大角数とした鍵穴をイメージすればいいのだ。素数以外は他の鍵でも代用されてしまう鍵。
原子核も日夜この鍵を探していると考えられる。
ご冥福をお祈り申し上げます。
円周率を、教えていただき有難う・・・
ダンシング・オールマス
マスするときはずむ心
ひとすじのきらめきにゆれる
すじひもがうるむ瞳の中で
無邪気に踊らせてみる
ダンシング・オールマス 言葉にすれば
ダンシング・オールマス 理に染まる
ダンシング・オールマス このままずっと
ダンシング・オールマス 瞳を閉じて
独り言吐息ひとつ
それだけで崩れてしまう
あぶなげな理としらず
ひらめきを夢見てた
ダンシング・オールマス 言葉にすれば
ダンシング・オールマス 理に染まる
ダンシング・オールマスこのままずっと
ダンシング・オールマス 瞳を閉じて
この賞で最後のマスを
どちらからともなくそう決めて
〇 ▫ をなぞるように踊る
初めて会ったマスのように
ダンシング・オールマス 言葉にすれば
ダンシング・オールマス 理に染まる
ダンシング・オールマス このままずっと
ダンシング・オールマス 瞳を閉じて
ダンシング・オールマス 言葉にすれば
ダンシング・オールマス 理に染まる
ダンシング・オールマス このままずっと
ダンシング・オールマス 瞳を閉じて
コメントを投稿
<< Home