量子ビット - quantum bit
NAMs出版プロジェクト: 量子ビット - quantum bit
http://nam-students.blogspot.jp/2017/08/quantum-bit.html
量子ビット - Wikipedia
https://ja.wikipedia.org/wiki/量子ビット
量子ビット(りょうしビット、英: quantum bit)とは、量子情報の最小単位のことである。キュービット、キュビット、クビット(英: qubit)、Qビット(英: Qbit)ともいう。それに対して、従来のコンピュータのビットの事を古典ビット(英: classical bit)やCビット(英: Cbit)という。
量子情報では、従来の情報の取扱量の最小単位であるビットの代わりに、情報を量子力学的2準位系の状態ベクトルで表現する。
古典ビットは0か1かのどちらかの状態しかとることができないが、量子ビットは、0と1だけでなく0と1の状態の量子力学的重ね合わせ状態もとることができる。ブラ-ケット記法では、1量子ビットは、と表現される。ここで、はの関係を満たす複素数である。これを観測した際に、状態を得る確率はであり、状態を得る確率はである。同じ記法で古典ビットを表現すると、は、どちらかが0で、もう一方が1である。
関連項目
量子コンピュータ - Wikipedia
https://ja.wikipedia.org/wiki/量子コンピュータ量子コンピュータ (りょうしコンピュータ、英語:quantum computer) は、量子力学的な重ね合わせを用いて並列性を実現するとされるコンピュータ。従来のコンピュータの論理ゲートに代えて、「量子ゲート」を用いて量子計算を行う原理のものについて研究がさかんであるが、他の方式についても研究・開発は行われている。
いわゆる電子式など従来の一般的な[1]コンピュータ(以下「古典コンピュータ」)の素子は、情報について、「0か1」などなんらかの2値をあらわす何れかの状態しか持ち得ない「ビット」で扱う。量子コンピュータは「量子ビット」 (qubit; quantum bit、キュービット) により、重ね合わせ状態によって情報を扱う。
n量子ビットあれば、の状態を同時に計算できる。もし、数千qubitのハードウェアが実現した場合、この量子ビットを複数利用して、量子コンピュータは古典コンピュータでは実現し得ない規模の並列コンピューティングが実現する。
量子コンピュータの能力については、計算理論上の議論と、実際に実現されつつある現実の機械についての議論がある。#計算能力の節を参照。
歴史
1980年代
量子コンピュータの歴史は、1980年に Paul Benioff が量子系においてエネルギーを消費せず計算が行えることを示した[2]ことに端を発し、1982年、ファインマンも量子計算が古典計算に対し指数関数的に有効ではないかと推測している[3]。これらに続き、1985年、ドイッチュは、「量子計算模型」と言える量子チューリングマシン[4]を定義し、1989年に量子回路[5]を考案した。
1990年代
1992年に、ドイッチュとジョサは、量子コンピュータが古典コンピュータよりも速く解ける問題でドイッチュ・ジョサのアルゴリズムを考案した[6]。 1993年に、ウメーシュ・ヴァジラーニと生徒のEthan Bernsteinは、万能量子チューリングマシンと量子フーリエ変換のアルゴリズムを考案した[7]。
1994年にピーター・ショアは、実用的なアルゴリズム『ショアのアルゴリズム[8]』を考案し、量子コンピュータの研究に火をつけた。これは、ヴァジラーニらの量子フーリエ変換や、同年のSimonの研究[9]を基礎に置いている。量子コンピュータ特有のアルゴリズムであるショアのアルゴリズムが、古典コンピュータでは現実的な時間で解くことができない素因数分解を、極めて短い時間で実行出来ることから、素因数分解の困難性を利用したRSA暗号の安全性は実用的な量子コンピュータが実現されれば崩れることを示した。
1995年に、アンドリュー・スティーン[10]やピーター・ショア[11]により、量子誤り訂正のアルゴリズムが考案された。 1996年に、ロブ・グローバーにより、その後、様々なアルゴリズムに応用されるグローバーのアルゴリズム[12]が考案された。同年、セルジュ・アロシュは、実験的観測によって量子デコヒーレンスを証明し、 [13] [14] 量子デコヒーレンスが量子コンピュータ実現への障害となることが実証された。 1997年に、Edward FarhiとSam Gutmannにより、量子ウォーク[15](Continuous-time quantum walk、略称: CTQW)が考案された。1998年に、量子コンピュータ用のプログラミング言語である、QCL (Quantum Computation Language) の実装が公開された。
また西森秀稔による、量子焼きなまし法の提案もこの時代であった。
2000年代
ハードウェア開発に大きな進展があり、2008年にイオントラップの専門家デービッド・ワインランドは、個々のイオンをレーザー冷却して捕捉することが出来ることを示し、個々の量子もつれ状態にあるイオンをマニピュレーションする、イオン・トラップ型量子コンピュータの研究が進展した。[16]
ショアのアルゴリズムは、2001年に核磁気共鳴[17]により、2007年に量子光学[18]により、2009年に光集積回路[19]により15の素因数分解 (=3*5) が実装された。
2010年代
2011年に突如として、カナダの企業D-Wave Systemsが量子コンピュータ「D-Wave」の建造に成功したと発表した。D-Waveはこの記事の多くの部分で説明している量子ゲートによるコンピュータではなく、量子焼きなまし法による最適化計算に特化した専用計算機である。発表当初のものは128量子ビットであった[20]。D-Waveが本当に量子コンピューティングを実現したものか否か、当初は疑う向きも多かったものの、確かに量子コンピューティングによるものとする調査論文が英科学誌ネイチャーに発表[21]されるなど、2014年10月現在、確実視される方向にある。
2012年、セルジュ・アロシュとデービッド・ワインランドがノーベル物理学賞を受賞した。受賞理由は「個別の量子系に対する計測および制御を可能にする画期的な実験的手法に関する業績」である。
エドワード・スノーデンの開示文書によると、NSAにおいて暗号解読のための実用化が研究されているとされる[22]。
2014年9月米グーグル社はUCLAのJohn Martinisと連携し量子コンピュータの独自開発を開始すると発表した[23]。
2016年5月、IBMは5量子ビットの量子コンピュータ[24]をオンライン公開した。デイヴィビッド・コーリー ウォータールー大学教授がテストした結果、ほぼ同じ結果を得ることができた[25]。
ソフトウェア
アルゴリズム
量子コンピュータ特有のアルゴリズムがいくつか知られており、伝統的に有名なものを示す。他の物は、Quantum Algorithm Zoo[26]などを参照。
ショアのアルゴリズム
ショアのアルゴリズム(英: Shor's factorizationとも)とは、素因数分解問題を高速に(多項式時間で)解くことができるアルゴリズムのことである。古典コンピュータでは非現実的な時間(準指数時間)で解くアルゴリズムしか知られていない。1994年にピーター・ショアによって発見された[8][27]。ショアは本件で、ネヴァンリンナ賞とゲーデル賞を受賞した。
2001年12月にIBMアルマデン研究所にて7qubitの量子コンピュータで15(=3×5)の素因数分解に成功した(Nature,12月20日発行号[17])。
少し改造することで離散対数問題(DLP,ElGamal暗号や楕円曲線暗号の安全性の根拠)も多項式時間で解くことができる。このアルゴリズムの基本的なアイデアを拡張したものが、可換隠れ部分群問題についての量子アルゴリズムである。現在は、これをさらに非可換隠れ部分群問題に拡張する研究が進展している。
ショアのアルゴリズムは、量子コンピュータが離散フーリエ変換を高速に実行できることによる。また、アルゴリズム全体は確率的(BQP)であり、正しい答えが得られるまで、何度も試行する。
N を因数分解するにあたり、a は N に対して素な数とし、a の mod N に関する位数、min{x|ax=1 (mod N)} を求める。つまり、ax の周期 r を求める。位数が高速に求められれば、因数分解は高速に行える。
例えば, N = 15 , a = 7 とする。
71 = 7 (mod 15)
72 = 4 (mod 15)
73 = 13 (mod 15)
74 = 1 (mod 15)
75 = 7 (mod 15)
76 = 4 (mod 15)
77 = 13 (mod 15)
78 = 1 (mod 15)
79 = 7 (mod 15)
...
7,4,13,1,7,4,13,1,7・・・という周期 4 の数列が生成される。
よって,周期 r = min{x|7x=1 (mod15)} = 4
手順の概略は以下の2つ。
- 全ての x に対して、均等な確率となるように初期化する。そして、それを axmod N のみ確率を持ち、それらは均等になるように変換する。この計算は量子コンピュータ的であるものの、基本的な考えは古典コンピュータと変わらない。そのために、2進数の足し算・引き算や、ビットによる条件分岐などを用意する。
- axmod N は周期 r を持つ。この周期が求める位数である。従って、1で得られた結果を離散フーリエ変換する。すると、周波数 1/r のところの確率が大きくなるので、観測すると、高い確率で r が得られる。失敗した場合は、成功するまで繰り返す。
グローバーのアルゴリズム



このアルゴリズムはデータ数に見合うだけ十分なqubit数があることを前提としているが、古典コンピュータにおいてデータに見合うだけの十分な並列度がある場合、f(z) = 1 を探すのはO(1)であり、関数の最小値を探す問題は、O(log log n) である。
ドイッチュ・ジョサのアルゴリズム
量子ウォーク
ランダムウォークを量子コンピュータ上で実行する。いくつかのアルゴリズムがこれを利用して作られている。
離散フーリエ変換
振幅に対して離散フーリエ変換を行うが、振幅は直接は観測できないことに注意が必要。ショアのアルゴリズムで使われている。QCLでのソースコードは以下の通り。変数 q を離散フーリエ変換している。V は conditional phase、H はアダマール変換である。
for i = 1 to #q { for j = 1 to i - 1 { V(pi / 2^(i - j), q[#q - i] & q[#q - j]); } H(q[#q - i]); } flip(q);プログラミング言語
量子コンピュータ用のプログラミング言語とその処理系の実装方法が多数提案されており、QCL[29]などがある。詳細は、量子プログラミング言語 を参照。
シミュレーター
量子コンピュータのアルゴリズムをシミュレーションにより実行するためのシミュレーターが多数作られている。一覧については、List of QC simulators[30]を参照。
ハードウェア
ハードウェアは量子ゲートを組み合わせた量子回路によって実現されるが、数学的に等価な量子ゲートが物理的には核磁気共鳴、量子光学、量子ドット、超伝導素子、レーザー冷却などによって構成出来るため、様々な実験的ハードウェアの実現法が研究されている。
核磁気共鳴・電子スピン共鳴
近年、核磁気共鳴(NMR)や電子スピン共鳴を用いた量子コンピュータの研究開発が行われている[17][31][32][33][34]。
2001年、7量子ビット量子コンピュータによる素因数分解が実装された[17][31]。核磁気共鳴 (NMR) により、1998年に2量子ビット、1999年に3量子ビット、2000年に5量子ビット、2001年に7量子ビット[32]、2005年に8量子ビットqubit[33]、2006年に12量子ビット[34]が実現した。1量子ビット増えるごとに並列度は2倍になる。
国内では大阪大学[35]や沖縄科学技術大学院大学[36]が主な研究拠点であり、核スピン・電子スピンを用いた量子情報処理の実験が行われている。
窒素空孔欠陥スピン・シリコン核スピン
国内では横浜国立大[37]、京大[38]が主な研究拠点であり、窒素空孔欠陥を用いた量子メディア変換・量子情報処理の実験が行われている。また慶応義塾大学[39] では、シリコン中の核スピンを用いた量子情報処理実験が行われている。
量子ドット
国内では理化学研究所[40] 、東京大学[41]が主な研究拠点であり、量子コンピュータの実現に向けた取り組みがなされている。
量子光学
特に光子を用いているものは光子コンピュータ、光量子コンピュータとも呼ばれる。 2001年、非線形光学を使わずに、量子コンピュータを作成する方法が考案された[42]。線形光量子コンピュータ (英: linear optical quantum computer、LOQC) と呼ばれ、その後の光量子コンピュータの主流となる。
2007年、光子を使い、4qubit量子コンピュータによる素因数分解が実装された[18]。さらに、2009年、光集積回路(シリコンフォトニクス)上で、4qubit量子コンピュータによる素因数分解が実装された[19]。
超伝導素子
超伝導素子を用いた量子コンピュータの量子ビットは、ジョセフソン・ジャンクションを用いた超伝導回路によって構成されている [43][44][45][46]。超伝導回路中の電荷(クーパー対)の自由度を用いた量子ビットを、電荷量子ビット、またはクーパー対箱と呼ぶ。1999年、日本電気において中村、Pashkin、蔡らにより実現された[43]。当時の量子ビットのコヒーレンス時間は約1ナノ秒であった。 超伝導量子ビットは回路量子電磁力学の研究とともに発展し、2004年には コプラナ導波路により実装された超伝導共振器と電荷量子ビットとの強結合が観測されている[47]。共振器や導波路を組み合わせた回路量子電磁力学は、超伝導量子ビット間の相互作用や、量子非破壊測定を行うとても良いツールとなっている。
SQUIDを含み、磁束量子の重ね合わせ状態を用いた量子ビットを磁束量子ビットと呼ぶ。2003年、デルフト工科大においてChiorescu、中村、Harmans、Mooijらにより実現された[44]。これらはDWAVE社が開発した量子焼きなまし法による最適化手法[20][21]に採用されている。
2007年に電荷量子ビットにおける電荷揺らぎ雑音を回避する量子ビットが提案され、トランズモン型量子ビットと呼ばれる[48]。比較的シンプルな構成で長コヒーレンス時間が実現され、米国を中心に盛んに研究が進められている。 2011年、量子計算や量子誤り訂正に必須となる単一試行の量子非破壊測定が実現し、トランズモン型超伝導量子ビットの量子跳躍が観測されている [49]。これらの技術の背景には、標準量子限界に近い雑音指数を達成する低雑音増幅器(ジョセフソンパラメトリック増幅器)の実現がある [50][51]。 2013年、上記の基礎技術とFPGAによる高速フィードバック処理により量子テレポーテーション[52]の実験が行われ、空間的に離れた量子ビット間の状態転送が実現した。 2014年には160マイクロ秒のコヒーレンス時間が実現し[53]、1999年の発見から15年の間に約10万倍という飛躍的な改善がなされている。 同年、Google社のJohn Martinis[54]らのグループは、誤り耐性符号の一つである表面符号の誤りしきい値を下回る、高い忠実度の基本量子ゲートを実現した[55]。これにより誤り耐性量子計算が現実化し、超伝導量子ビットを用いた量子計算機の開発が一層加速することになる。 2015年、9量子ビットによるビット反転エラー訂正を実行し、論理量子ビットのエラー確率を物理量子ビットに比べ約1/8まで小さくすることに成功した[56]。 同年には、新しい機能性材料の開発を飛躍的に加速する、フェルミ粒子のディジタル量子シミュレーションが、小さな系にて実装されている[57]。 大規模化に向けた取り組みが始まり、2016年には三次元集積技術による実装が議論されている[58]。
国内では東京大学[59]と理化学研究所[60]が量子コンピュータや量子情報処理の研究を、NTT物性科学基礎研究所[61]、 情報通信研究機構[62]が量子物理の研究を行っており、主な研究拠点である。
海外ではGoogle[54]、IBM[63]、デルフト工科大学(インテル・マイクロソフトが支援)[64]、マサチューセッツ工科大学[65]、チューリッヒ工科大学[66]が主な研究拠点である。
イオントラップ
イオントラップを用いる量子コンピュータでは、レーザー冷却によってイオンの捕捉とマニピュレーションを行なう。 国内では阪大[67]にて量子シミュレータ・量子コンピュータに向けた研究がなされている。
その他
量子回路
量子ゲート
古典コンピュータでの計算は、ブール論理にもとづいた論理ゲートによる論理演算をベースとして行われる。これに対し、量子コンピュータの量子回路では、量子演算の演算子に対応する演算を行うゲートは量子ゲートと呼ばれ、ユニタリー行列でなくてはならない。任意の1量子ビットに対するユニタリー行列は以下の形式で表現できる。可逆計算であることも特徴である。
1量子ビットに対する任意のユニタリー変換とCNOTゲートの組合せによって、n量子ビットの場合も任意のユニタリ変換を構成出来ることが知られている。
NOT
NOTはパウリ行列の1つでもある。
スワップ
制御NOT
CNOTと呼ばれる。XORに相当する。
パウリ行列
アダマール変換

Conditional Phase
CPhaseと呼ばれる。
1量子ビットの場合は、以下の通り。
回転
トフォリゲート
フレドキンゲート
計算能力
理論
ヴァジラーニらは、量子チューリングマシンと古典チューリングマシンの計算可能性が等価であることを示した。したがって、計算可能性の点では既存のあらゆるコンピュータと量子チューリングマシンは変わらない。一方で、やはり、古典チューリングマシンで原理的に解くことができない問題は量子チューリングマシンにも解くことはできない。
計算可能性の理論に関しては以上のようであるのだが、では、計算複雑性の理論としてはどうだろうか、というのが関心のある所であろう。
量子コンピュータは容易に古典コンピュータをエミュレートすることが可能であるため、古典コンピュータで速く解ける問題は、量子コンピュータにも速く解くことができる。よって、量子コンピュータは古典コンピュータ「以上」に強力な計算速度を持つ。つまりは完全な上位互換である。「より大きい」かどうかはよくわかっていない。量子コンピュータに関係する複雑性クラスにBQPがある。BQPはPを含むが、NPとBQPの関係は2016年現在わかっていない(詳細はBQPの記事を参照)。
実際
量子ゲートマシンでは、理論的には古典コンピュータに重ね合わせを扱う能力を持たせた、「上位互換」のコンピュータを作ることもできるかもしれないが、2017年現在始まっているIBM Q[68]などではまだごく限られた数の量子ビットしか扱えず、既に提案されよく知られている量子アルゴリズムの実証といった限られたタイプの計算から行われるものと思われる。
D-Waveなどの量子アニーリングやその他いくつかのタイプが提案されている、量子イジングマシンは一種の専用計算機に近いものと言える。
参考文献
- ^ 一般的でない例としては、数は少ないが3状態の素子で動作するコンピュータや、多値論理の応用などとして研究されている。MLC NANDフラッシュのように実用例も一部にはある。
- ^ Paul Benioff (1980年5月). “The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines” (English). J. Stat. Phys.. doi:10.1007/BF01011339. 2017年4月1日閲覧。
- ^ Richard Feynman , Peter W. Shor (1982年). “Simulating Physics with Computers” (English). SIAMコンピュータジャーナル . doi:10.1.1.45.9310. 2017年4月1日閲覧。
- ^ David Deutsch (1985年). “Quantum theory, the Church-Turing principle and the universal quantum computer” (English). ペンシルベニア州立大学. doi:10.1.1.125.4866. 2017年4月1日閲覧。
- ^ Royal Society (1989年9月8日). “Quantum computational networks”. JSTOR. 2017年4月1日閲覧。
- ^ Deutsch, David; Jozsa, Richard (1992年12月). “Rapid Solution of Problems by Quantum Computation” (English). en:Astrophysics Data System. doi:10.1098/rspa.1992.0167. 2017年4月1日閲覧。
- ^ Ethan Bernstein , Umesh Vazirani (1993年). “Quantum complexity theory” (English). ペンシルベニア州立大学. doi:10.1.1.144.7852. 2017年4月1日閲覧。
- ^ a b Peter W. Shor, "Algorithms for Quantum Computation: Discrete Logarithms and Factoring", In Proceeding of 35th IEEE FOCS, pp.124-134, Santa Fe, NM, Nov 20-22, 1994. (ショアのアルゴリズムの論文)
- ^ Daniel R. Simon (1994年). “On the Power of Quantum Computation”. ペンシルベニア州立大学. doi:10.1.1.51.5477. 2017年4月1日閲覧。
- ^ Andrew Steane (1996年5月13日). “Multiple Particle Interference and Quantum Error Correction” (English). コーネル大学図書館. コーネル大学. doi:/ rspa.1996.0136 10.1098 / rspa.1996.0136. 2017年4月1日閲覧。
- ^ A. R. Calderbank, Peter W. Shor (1996年4月16日). “Good Quantum Error-Correcting Codes Exist” (English). コーネル大学図書館. コーネル大学. doi:10.1103/PhysRevA.54.1098. 2017年4月1日閲覧。
- ^ a b Lov K. Grover, "A fast quantum mechanical algorithm for database search", STOC'96, pp.212-219, Philadelphia, Pennsylvania, United States, May 22-24, 1996. (グローバーのアルゴリズムの論文)
- ^ Serge Haroche, Jean-Michel Raimond & Michel Brune ; Le chat de Schrödinger se prête à l'expérience - Voir en direct le passage du monde quantique au monde classique, La Recherche 301 (Septembre 1997) 50 (disponible en ligne)
- ^ Serge Haroche ; Une exploration au cœur du monde quantique, dans : Qu'est-ce que l'Univers ?, Vol. 4 de l'Université de Tous les Savoirs (sous la direction d'Yves Michaux), Odile Jacob (2001) 571.
- ^ Edward Farhi (MIT), Sam Gutmann (Northeastern) (1998年3月20日). “Quantum Computation and Decision Trees” (English). コーネル大学図書館. コーネル大学. doi:10.1103/PhysRevA.58.915. 2017年4月1日閲覧。
- ^ Christopher R. Monroe en David J. Wineland. (2008年8月11日). “Quantum Computing with Ions” (English). サイエンティフィック・アメリカン. 2017年4月1日閲覧。
- ^ a b c d “Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance”. 2016年6月17日閲覧。
- ^ a b Demonstration of Shor's quantum factoring algorithm using photonic qubits
- ^ a b Shor's Quantum Factoring Algorithm on a Photonic Chip
- ^ a b “Learning to program the D-Wave One”. 2013年6月閲覧。
- ^ a b Sergio Boixo, Tameem Albash, Federico M. Spedalieri, Nicholas Chancellor & Daniel A. Lidar. “Experimental signature of programmable quantum annealing” (English). ネイチャー. doi:10.1038/ncomms3067. 2013年6月閲覧。
- ^ Steven Rich; Barton Gellman (2014年1月3日). “NSA seeks to build quantum computer that could crack most types of encryption” (English). The Washington Post 2014年1月9日閲覧。
- ^ 中田 敦(日経コンピュータ) (2014年9月3日). “米グーグル、量子コンピュータの独自開発に乗り出す”. ITpro (日経BP). オリジナルの2014年9月3日時点によるアーカイブ。2017年4月1日閲覧。
- ^ ニューヨーク州ヨークタウンハイツの研究所に存在する。
- ^ “「誰でも使える量子コンピューター」IBMが公開する意味”. WIRED (コンデナスト・パブリケーションズ). (2016年5月9日). オリジナルの2016年5月9日時点によるアーカイブ。 2017年4月1日閲覧。
- ^ http://www.its.caltech.edu/~sjordan/zoo.html
- ^ Peter W. Shor, "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer", SIAM Journal on Computing, Vol.26, No.5, pp.1484-1509, Oct 1997. (ジャーナル版)
- ^ Lov K. Grover, "Rapid sampling though quantum computing", STOC'00, pp.618-626, Portland, Oregon, United States, May 21-23, 2000. (グローバーの新アルゴリズム)
- ^ http://tph.tuwien.ac.at/~oemer/qcl.html
- ^ http://www.quantiki.org/wiki/index.php/List_of_QC_simulators
- ^ a b “IBM's Test-Tube Quantum Computer Makes History”. 2016年6月17日閲覧。
- ^ a b “量子バイトを実現――量子コンピューティングへの大きな一歩”. 2016年6月17日閲覧。
- ^ a b “Benchmarking quantum control methods on a 12-Qubit system”. Phys. Rev. Lett. 96: 170501. (2006). doi:10.1103/PhysRevLett.96.170501.
- ^ “大阪大学 基礎工学研究科 システム創成専攻 量子情報デバイス研究室”. 2016年5月13日閲覧。
- ^ “沖縄科学技術大学院大学 量子ダイナミクスユニット”. 2016年5月14日閲覧。
- ^ “横浜国立大学 大学院 工学研究院 物理情報工学専攻”. 2016年5月13日閲覧。
- ^ “京都大学 化学研究所”. 2016年5月13日閲覧。
- ^ “慶應義塾大学理工学部物理情報工学科”. 2016年5月13日閲覧。
- ^ “量子機能システム研究グループ”. 2016年5月13日閲覧。
- ^ “東京大学大学院 工学系研究科 物理工学専攻”. 2016年5月13日閲覧。
- ^ A scheme for efficient quantum computation with linear optics
- ^ a b Nakamura, Yasunobu; Pashkin, Yu. A.; Tsai, J. S. (April 29, 1999). “Coherent control of macroscopic quantum states in a single-Cooper-pair box”. Nature 398: 786-788. doi:10.1038/19718.
- ^ a b Chiorescu, I.; Nakamura, Y.; Harmans, C. J. P. M.; Mooij, J. E. (Mar 21, 2003). “Coherent Quantum Dynamics of a Superconducting Flux Qubit”. Science 299: 1869-1871. doi:10.1126/science.1081045.
- ^ Clarke, John; Wilhelm, Frank (June 19, 2008). “Superconducting quantum bits”. Nature 453: 1031-1042. doi:10.1038/nature07128.
- ^ Kaminsky, William M (2004年). “Scalable Superconducting Architecture for Adiabatic Quantum Computation”. arXiv:quant-ph/0403090 [quant-ph].
- ^ “Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics”. Nature 431: 162-167. (2004). doi:10.1038/nature02851.
- ^ “Charge-insensitive qubit design derived from the Cooper pair box”. Phys. Rev. A 76: 042319. (2007). doi:10.1103/PhysRevA.76.042319.
- ^ “Observation of Quantum Jumps in a Superconducting Artificial Atom”. Phys. Rev. Lett. 106: 110502. (2011). doi:10.1103/PhysRevLett.106.110502.
- ^ “Nonlinearities and parametric amplification in superconducting coplanar waveguide resonators”. Appl. Phys. Lett. 90: 253509. (2007).
- ^ “Flux-driven Josephson parametric amplifier”. Appl. Phys. Lett. 93: 042510. (2008).
- ^ “Deterministic quantum teleportation with feed-forward in a solid state system”. Nature 500: 319–322. (2013). doi:10.1038/nature12422.
- ^ “Excited state population of a 3D transmon in thermal equilibrium”. 2016年5月13日閲覧。
- ^ a b “Martinis Group”. 2016年5月14日閲覧。
- ^ “Superconducting quantum circuits at the surface code threshold for fault tolerance”. Nature 508: 500–503. (2014). doi:10.1038/nature13171.
- ^ Kelly, J.; Barends, R.; Fowler, A. G.; Martinis, John M; et, al. (2015). “State preservation by repetitive error detection in a superconducting quantum circuit”. Nature 519: 66–69. doi:10.1038/nature14270.
- ^ “Digital quantum simulation of fermionic models with a superconducting circuit”. Nature Communications 6: 7654. (2015). doi:10.1038/ncomms8654.
- ^ “3D Integration for Superconducting Qubits”. 2016年5月13日閲覧。
- ^ “東京大学 先端科学技術研究センター 量子情報物理工学分野”. 2016年5月13日閲覧。
- ^ “理化学研究所 創発物性科学研究センター 超伝導量子エレクトロニクス研究チーム”. 2016年5月13日閲覧。
- ^ “NTT物性科学基礎研究所”. 2016年5月13日閲覧。
- ^ “情報通信研究機構 未来ICT研究所 フロンティア創造総合研究室”. 2016年5月13日閲覧。
- ^ “IBM Quantum Computing”. 2016年5月14日閲覧。
- ^ “デルフト工科大学 Superconducting quantum circuits”. 2016年5月14日閲覧。
- ^ “マサチューセッツ工科大学 Superconducting Circuits and Quantum Computation group”. 2016年5月14日閲覧。
- ^ “チューリッヒ工科大学 Quantum Device Lab”. 2016年5月14日閲覧。
- ^ “大阪大学 大学院基礎工学研究科 電子光科学領域 量子エレクトロニクスグループ”. 2016年5月14日閲覧。
- ^ https://www.research.ibm.com/ibm-q/
関連項目
外部リンク
量子コンピュータの仕組みをエクセルで理解してみよう ~量子アニーリングの古典版「シミュレーテッドアニーリング」の実装~ (1/4):CodeZine(コードジン)
http://codezine.jp/article/detail/9491前回は、量子コンピュータの基本的な考え方である、0と1の重ね合わせ状態を使って高速計算を実現する方法と、量子コンピュータの一方式である「量子アニーリング」の動作原理について簡単に説明しました。今回は、量子コンピュータの動作をより直感的に理解することをめざして、エクセルVBAを用い、量子アニーリングの古典版である「シミュレーテッドアニーリング」というアルゴリズムを作ってみます。

| 目次 |
|---|
普通のコンピュータが解けない問題とは?
第1回において、機械学習などの分野では、普通のコンピュータでは現実的な時間で解くことができない問題が多く存在し、そういった問題を解くことができる可能性を量子コンピュータに見出している、と説明しました。今回のテーマであるエクセルによる実装の前に、まずはこの“解けない問題”についてもう少し詳しく説明し、普通のコンピュータが“できないこと”とは何かを明確にしましょう。
まず、ここで言う“解けない問題”とは、正確には「多項式時間での解法が知られていない」問題と定義されます。「多項式時間ってなんですのん?」と思う人多数でしょう。順を追って説明しましょう。まず、下の図を見てください。
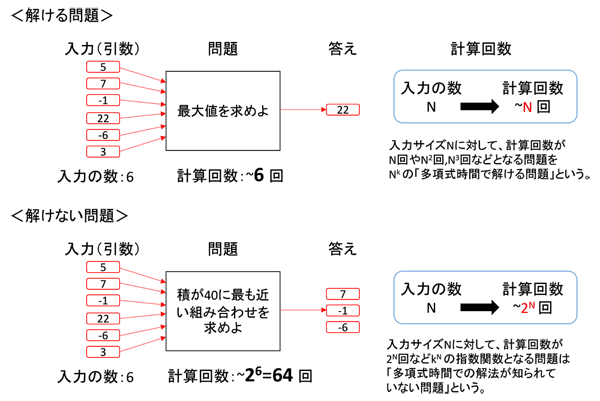
どんな問題にも、必ず入力があります。プログラムでいうところの“引数”です。そして、解ける問題とは、入力(引数)の数(入力サイズ)に対して計算しなければならない回数がそれほど多くならない問題のことです。例えば「入力の数の中から最大値を求めよ」という問題は、入力の数が6個の場合、1つずつ大小関係を比較するという計算をしていくとおよそ6回の計算で解が求まります。入力の数が10個なら10回、100個なら100回ですから、問題「最大値を求めよ」の計算回数は入力サイズNに対してN回の計算回数が必要です。
他にも「入力の数の合計を求めよ」もN回、「入力の数の中から剰余が最大となる2つのペアを選び出せ」は、総当たり戦のように2つのペアをすべて計算すればよいのでおよそN2回など、我々の身の回りにある問題の多くはNk(k:整数)の多項式で計算回数を見積もることができます。こういった、およそNk回の計算回数となるような問題を、Nの多項式で計算時間を見積もることができることから、「多項式時間で解ける問題」と呼びます。
一方、「多項式時間での解法が知られていない問題」とはどんな問題でしょうか。例えば「入力の数において、積が40に最も近い組み合わせを求めよ」という問題があったとします。どう解けばよいでしょう。普通に考えると、入力の数のすべての組み合わせを書き出して、積を計算し、40に最も近いものを探すことになるでしょう。組み合わせは、入力の数が6個であれば、26=64個あります。つまり、64回掛け算の計算をして40に最も近い組み合わせを探す必要があります。この問題は、入力の数が10個の時は210=1,024回、20個の時は220=1,048,576回、30個の時は230=1,073,741,824とどんどん増えていきます。
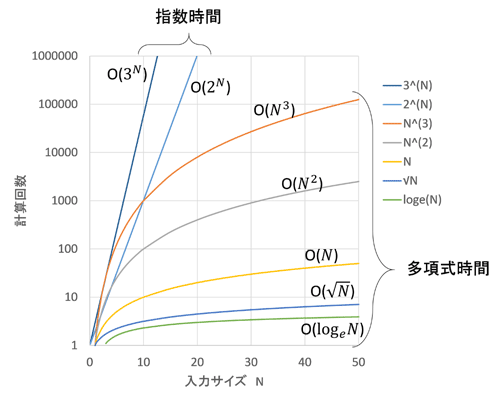
入力サイズNに対して、kN(k:整数)回の計算回数を必要とする、つまり指数関数的に計算回数が増加していくような問題を「多項式時間での解法が知られていない問題」と言って、普通のコンピュータで“解けない問題”と呼んでいるのです。実際には、入力サイズが小さければ指数関数的な計算回数でも解くことができるので、くどさをいとわず言えば、「普通のコンピュータで“入力サイズが大きくなってくると、急激に計算回数が増加して”解けない問題」となります(下図参照)。こういった問題に対して量子コンピュータの出番となるわけです。



























5 Comments:
【技術】東大“究極の量子コンピューター” へ 基本原理開発に成功 [無断転載禁止]©2ch.net
87コメント34KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1ノチラ ★2017/09/22(金) 22:07:53.05ID:CAP_USER>>44>>54>>58
離れた物質の間を情報が瞬間移動する「量子テレポーテーション」と呼ばれる現象を利用して、現代のスーパーコンピューターをはるかにしのぐ新型の量子コンピューターの基本原理の開発に成功したと東京大学の研究チームが発表しました。
量子コンピューターをめぐっては、NASAやグーグルが別の原理で作られたカナダのベンチャー企業の実用化モデルを購入し研究を進めていますが、研究チームは今回の基本原理を使えばこれを大きく上回る性能の究極の量子コンピューターを生み出せるとしています。
現代のスーパーコンピューターをはるかに上回る新型の量子コンピューターの基本原理の開発に成功したのは、東京大学の古澤明教授の研究チームです。
研究チームは、2つの離れた物質の間で情報が光の速度で瞬間移動する「量子テレポーテーション」と呼ばれる現象に注目しました。
この現象は量子と呼ばれる光の粒など極めて小さな世界で起きるもので、アインシュタインはこれを引き起こすものを「奇妙な遠隔作用」と呼んでいました。
例えば光の粒を人工的に2つに分けて離れた位置に置き、一方に2、もう一方に+2という情報を与えます。
続いてこの2つの光の粒を互いに「量子もつれ」、アインシュタインがいう「奇妙な遠隔作用」が働く状態にすると情報が光の速度で瞬間移動し、光の粒が4という情報を持つようになるのです。
情報の伝え方は現在、足し算、引き算、かけ算、割り算が可能で、今回、研究チームは、光の粒をループ状の回路の中で回しながら瞬時の計算を行える光の粒を100万個同時に作り出すことに成功したということで、超高速の量子コンピューターを作り出す基本原理を開発できたとしています。
今のところ光の粒1組を「量子もつれ」の状態にして計算を行うために縦4メートル横2メートルの装置が必要ですが、新たな基本原理を使えば、今の半分ほどの大きさの装置でほぼ無限に計算を繰り返せる究極の量子コンピューターを生み出せるようになるとしています。
古澤教授は「今まで提案されていない全く新しい方式で、本当の意味での量子コンピューターの実現につながると思う。欧米の後追いでなく、日本で生まれた日本方式で究極の量子コンピューターをつくりたい」と話しています。
幅広い社会問題解決 経済的にも大きな利益
量子コンピューターをめぐっては幅広い社会の問題を解決に導き経済的にも大きな利益をもたらす可能性を秘めているとして、欧米各国でも大手企業が相次いで研究・開発に名乗りを上げています。
このうちドイツの自動車メーカーのフォルクスワーゲンは、「アニーリングマシン」と呼ばれるタイプの量子コンピューターを実用化したカナダのベンチャー企業D-WaveSystems社と共同で量子コンピューターを使って道路の渋滞を解消する研究をことし3月に発表しました。この研究は中国の北京で400台余りのタクシーが、一斉に街の中心部から空港に行くとき、渋滞を防ぎながら最短時間で到着するルートを導き出すもので、これまで自社が持っていた高性能のコンピューターでは、結果を出すのに30分かかりましたが、量子コンピューターでは、わずか数秒だったということです。将来の自動運転システムなどに応用できるとしています。
またこのアニーリングマシンの基本原理を開発した東京工業大学の西森秀稔教授によりますとアメリカのマイクロソフトは、量子コンピューターで小さな分子の運動を解析し、新たな組み合わせの化合物を作り出す「量子化学計算」と呼ばれる研究を進めています。例えば世界中で農業に使われる肥料を量子化学計算によって効率的に作り出す方法が見つかれば、肥料を生産するために出される二酸化炭素の量を大きく減らし地球温暖化などの環境問題の解決に役立つということです。
アメリカが進めているアニーリングタイプの量子コンピューターの国家プロジェクトに日本人として唯一参加している西森教授は「アメリカやカナダではしれつな競争が目に見える形で始まっていて、そこにヨーロッパや中国も大がかりな投資を始め、スタートの号砲が鳴ったという状態だ。通常のコンピューターでできないものも量子コンピューターを使えばできるということで、経済的な効果が大きいことに気付いた大企業の間で開発が加速している」と指摘しています。
http://www3.nhk.or.jp/news/html/20170922/k10011152541000.html
【IT】量子コンピュータのエラー、通常のPCで計算可能 東大が研究
11コメント3KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1しじみ ★2017/11/13(月) 21:41:30.42ID:CAP_USER
東京大学の研究グループはこのほど、量子コンピュータの内部で発生したエラーを、
一般的なデスクトップPCで正確に高速で計算できる手法を開発したと発表した。量子的なエラーを粒子の運動に捉え、
通常のPCでも計算可能にした。実用的な量子コンピュータの開発に役立つという。
量子コンピュータは、量子ビットという情報単位を用いる。0と1に加え、0と1の「重ね合わせ状態」(量子の重ね合わせ)を表すことができ、
よりたくさんの値を扱えるため従来の計算や解析を短時間で行えるといい、米MicrosoftやGoogleなどが実用化を目指している。
量子ビットには、0と1が入れ替わる通常のエラー以外に、0と1の「重ね合わせ」の比率が少しだけずれる特有のエラーがある。
量子コンピュータの開発には、このエラーを訂正しながら計算を続ける仕組み「量子誤り訂正」が必要だが、
エラーをどの程度減らせば訂正がうまくいくかを見積もるには計算量が膨大になり、
「量子コンピュータの実現には量子コンピュータが必要」というジレンマに陥る可能性があった。
研究グループは、量子誤り訂正が「フェルミ粒子」の運動を表したモデルが当てはまることを発見。
この運動は通常のPCでもシミュレートできるため、エラーに対応する粒子の運動を計算すれば、
量子コンピュータが正しく誤りを訂正できているかを確かめられるという。
研究成果は、米科学誌「Physical Review Letters」(オンライン版)に11月9日付で掲載された。
ITmedia NEWS
http://www.itmedia.co.jp/news/articles/1711/13/news113.html
2名無しのひみつ2017/11/13(月) 22:00:29.09ID:7D3Fb8LS>>3
猫は生きていた?
3名無しのひみつ2017/11/13(月) 22:07:57.38ID:tdN36pVh>>4
>>2
俺のはハエと合体してた
4名無しのひみつ2017/11/13(月) 22:10:26.58ID:9MYX47oA
>>3
後のキャットフライである
5名無しのひみつ2017/11/13(月) 22:15:43.35ID:0fqtn/zR
なまこ?
6名無しのひみつ2017/11/13(月) 22:31:36.11ID:+e+7hTDR
>従来の計算や解析を短時間で行えるといい、
πの計算は高速にできないからちょっとウソ
7名無しのひみつ2017/11/13(月) 22:34:29.80ID:Vmw/9u1P
なんでも計算できるわけじゃないんだろう?
8名無しのひみつ2017/11/13(月) 22:39:07.64ID:JLe8s501
exelの結果を電卓で確認
【半導体】ムーアの法則の限界を突破する「金属-空気トランジスタ」が半導体を置き換える可能性[12/03]
56コメント17KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1しじみ ★2018/12/03(月) 21:32:39.63ID:CAP_USER>>29>>32
「ムーアの法則」の限界がささやかれている半導体に代わって、新たに「Metal-Air Transistor(金属-空気トランジスタ)」と呼ばれる技術が開発されています。金属-空気トランジスタが実現することで、ムーアの法則はあと20年間は維持されると言われています。
Metal–Air Transistors: Semiconductor-Free Field-Emission Air-Channel Nanoelectronics - Nano Letters (ACS Publications)
https://pubs.acs.org/doi/10.1021/acs.nanolett.8b02849
New Metal-Air Transistor Replaces Semiconductors - IEEE Spectrum
https://spectrum.ieee.org/nanoclast/semiconductors/devices/new-metalair-transistor-replaces-semiconductors
Intel創業者のゴードン・ムーア氏が提唱した、「半導体集積回路のトランジスタ数は18カ月(のちに2年に修正)ごとに倍増する」という経験則は、半導体産業全体で開発目標とされ、その通りに微細化技術が開発されて半導体の性能が向上してきました。しかし、回線幅が原子レベルに近づく中、ムーアの限界を維持することは困難になり、ムーアの法則は遅くとも2025年に物理的限界に達して実現不可能になるという状態になっています。
そんな中、オーストラリアのRMIT大学の研究者が、金属ベースの空気チャンネルトランジスタ(ACT)を開発しました。ACTは電荷ベースの半導体とは違い、35ナノメートル未満のエアギャップ(空気層)によって分離したソースとドレインそれぞれの対面式金属ゲートを使うことで、基板から垂直方向にトランジスタネットワークを構築する技術だとのこと。エアギャップは空気中の電子の平均自由行程よりも小さいので、電子は飛散することなく室温中で空気中を移動することができます。
微細化の追求を止め、立体構造にフォーカスを当てることで、ACTでは単位面積当たりのトランジスタ数を増加させることができます。ACTを開発中のシュルチ・ニランター博士は、「シリコンバルクに縛られたこれまでのトランジスタと異なり、私たちの開発するデバイスは、基板からボトムツートップで製造できるアプローチです。最適なエアギャップを作ることさえできれば、完全な3Dトランジスタネットワークを構築できます」と述べています。
トランジスタの主材料に、半導体ではなく金属と空気を用いることは、エミッタやコレクタを敷き詰めるのが1つのプロセスで可能な点、既存のシリコン製造プロセスをACTの製造に流用できる点、ドーピング・熱処理・酸化などのシリコン半導体で不可欠な処理が不要なため、処理工程が半導体に比べて大幅に少なくなり、製造コストを大幅に削減できる点などでも大きなメリットがあるとニランター博士は強調しています。
その上、シリコンを金属で置き換えることで、どんな誘電体表面にもACTを作ることができる可能性があり、超薄型のガラスやプラスチックにデバイスを構築することで柔軟で体に着用できる技術にも応用できると期待されています。
ACTについて研究者らは概念実証を終えたため、今後は様々なソース+ドレイン構成をテストするステップに進むとのこと。より耐久性のある材料を使って安全性を高め、コンポーネントの効率を向上させるために、リソグラフィや成膜の技術や、ベースとなる金属の選定が行われる予定です。なお、ACTの理論速度は、現在の半導体デバイスが動作するスピードの約1万倍となるTHz(テラヘルツ)の領域にあるとのことで、これから10年間で商用レベルの電解放出空気チャンネルトランジスタを開発するという比較的、余裕のあるロードマップを描いているそうです。
https://i.gzn.jp/img/2018/12/03/metal-air-transistor/a02_m.jpg
サムネイル読み込み中···
GIGAZINE
https://gigazine.net/news/20181203-metal-air-transistor/
【IT】データサイエンティスト職に求められる言語のトップに「Python」--「R」を上回る
76コメント26KB
全部
1-100
最新50
★スマホ版★
■掲示板に戻る■
★ULA版★
1田杉山脈 ★2019/01/12(土) 18:37:50.17ID:CAP_USER>>23
「Python」と「R」はデータサイエンティスト職の求人で最も多く要求されるスキルに数えられている。ところが、こうしたプロフェッショナルの仕事で最も頻繁に使用されているプログラミング言語について調査した複数の報告書によると、実際は評価が分かれるという。Cloud Academyの米国時間12月27日付の報告書で明らかになった。
まず、TIOBE Programming Community Indexによれば、2018年の検索エンジンのリクエスト数でみたRの順位は下降気味だったという。だが、データプロフェッショナル1万6000人を対象に実施したKaggleの調査では、全体で最も人気の高いプログラミング言語はPythonであるものの、統計およびデータサイエンティストは他のどの職務よりも業務でRを使用している割合が高いことが分かった。データサイエンティストの87%はPythonを、71%はRを業務で使用していると回答していると、同報告書に記
以下ソース
https://japan.techrepublic.com/article/35131060.htm
ⅯⅮ
MDはローマ数字で1500を意味する
(ローマ数字←→アラビア数字変換)
http://www.cam.hi-ho.ne.jp/mendoxi/misc/roman-arabic.html
ローマ数字にはそれに対応した特殊文字コードがある
http://www.htmq.com/text/8000-8999.shtml
コメントを投稿
<< Home